
分析 (1)由题意可得$\frac{3a-3}{9-a}$≤0 ①,且 $\frac{5a-3}{25-a}$>0 ②,分别求得①和②的解集,再取交集,记得所求.
(2)由题意可得$\frac{3}{a}$<1,且 $\sqrt{a}$>$\frac{3}{a}$,不等式即$\frac{a(x-\frac{3}{a})}{(x-\sqrt{a})(x+\sqrt{a})}$≤0,用穿根法求得它的解集.
解答 解:(1)关于的不等式$\frac{ax-3}{{x}^{2}-a}$≤0的解集为M,若3∈M,且5∉M,
则有$\frac{3a-3}{9-a}$≤0 ①,且 $\frac{5a-3}{25-a}$>0 ②,解①求得 a≤1 或a>9,
解②求得 $\frac{3}{5}$<a<25,
故原不等式的解集为($\frac{3}{5}$,1]∪(9,25).
(2)若a>3,则由不等式$\frac{ax-3}{{x}^{2}-a}$≤0 可得$\frac{3}{a}$<1,且 $\sqrt{a}$>$\frac{3}{a}$,
不等式即$\frac{a(x-\frac{3}{a})}{(x-\sqrt{a})(x+\sqrt{a})}$≤0,
用穿根法求得它的解集为(-∞,-$\sqrt{a}$)∪[$\frac{a}{3}$,$\sqrt{a}$).
即集合M=(-∞,-$\sqrt{a}$)∪[$\frac{a}{3}$,$\sqrt{a}$).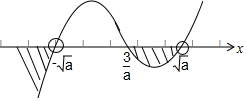
点评 本题主要考查分式不等式、一元二次不等式的解法,体现了转化的数学思想,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
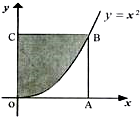
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com