
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
分析 (1)利用平均数公式计算即得.
(2)把所给的7对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.
(3)作出利用最小二乘法来求线性回归方程的系数的量,求出横标和纵标的平均数,求出系数,即可求出回归方程.
解答 解:(1)$\overline{x}$=$\frac{1}{7}$(3+4+5+6+7+8+9)=6,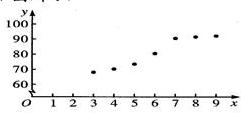
$\overline{y}$=$\frac{1}{7}$(66+69+73+81+89+90+91)≈79.86;
(2)把所给的7对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.
(3)∵3×66+4×69+5×73+6×81+7×89+8×90+9×91=3487,
32+42+52+62+72+82+92=280,
∴$\stackrel{∧}{b}$=$\frac{3487-7×6×\frac{559}{7}}{280-7×36}$=4.75,$\stackrel{∧}{a}$=$\frac{559}{7}$-6×4.75≈51.36,
故线性回归方程为$\stackrel{∧}{y}$=4.75x+51.36.
点评 本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法做出线性回归方程的系数,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
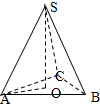 如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com