
【题目】如图,已知四棱台![]() 上、下底面分别是边长为3和6的正方形,
上、下底面分别是边长为3和6的正方形,![]() ,且
,且![]() 底面
底面![]() ,点
,点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上.
上.
(1)若是![]() 是
是![]() 的中点,证明:
的中点,证明:![]() ;
;
(2若![]() //平面
//平面![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,求四面体
,求四面体![]() 的体积
的体积
【答案】由题意得, A A 1 , A B , A D 两两垂直,以 A 为坐标原点, A B , A D , A A 1 所在直线分别为 x 轴 y 轴 z 轴,建立如图下图所示的空间直角坐标系,则相关各点的坐标为 A ( 0 , 0 , 0 ) , B 1 ( 3 , 0 , 6 ) , D ( 0 , 6 , 0 ) , D 1 ( 0 , 3 , 6 ) , Q ( 6 , m , 0 ) , 其中 m = B Q , 0 ≤ m ≤ 6 .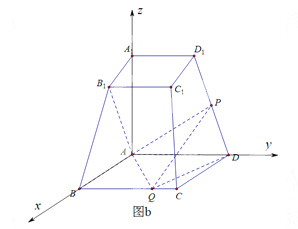
(1)若![]() 是
是![]() 的中点,则
的中点,则![]() 于是
于是![]() 所以
所以![]() .即
.即![]()
(2)由题意设知,![]() 是平面
是平面![]() 内的两个不共线向量.设
内的两个不共线向量.设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则 即
即![]() ,取
,取![]() 得
得![]() ,又平面
,又平面![]() 的一个法向量
的一个法向量![]() 所以
所以![]()
![]() 而二面角P-QD-A的余弦值为
而二面角P-QD-A的余弦值为![]() , 因此
, 因此![]() =
=![]() 解得.m=4或者m=8(舍去)此时Q(6,4,0)设
解得.m=4或者m=8(舍去)此时Q(6,4,0)设![]() 而
而![]() =(0,-3,6)由此得点P
=(0,-3,6)由此得点P![]()
![]() 因为PQ//平面ABB1A1且平面ABB1A1的一个法向量
因为PQ//平面ABB1A1且平面ABB1A1的一个法向量![]() =(0,1,0)所以,
=(0,1,0)所以,![]() ·
·![]() =0即,
=0即,![]() 亦即得
亦即得![]() 从而P(0,4,4,)于是将四面体ADPQ视为以
从而P(0,4,4,)于是将四面体ADPQ视为以![]() ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积
ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积![]()
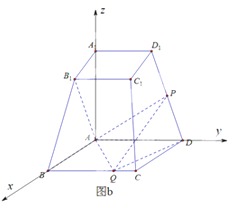

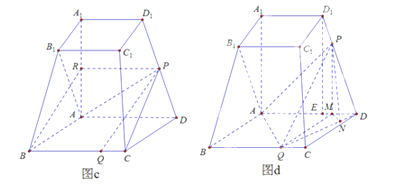

【解析】由题意得,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴
轴![]() 轴
轴![]() 轴,建立如图下图所示的空间直角坐标系,则相关各点的坐标为
轴,建立如图下图所示的空间直角坐标系,则相关各点的坐标为![]() 其中
其中![]() .
.
(1)若![]() 是
是![]() 的中点,则
的中点,则![]() 于是
于是![]() 所以
所以![]() .即
.即![]()
(2)由题意设知,![]() 是平面
是平面![]() 内的两个不共线向量.设
内的两个不共线向量.设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则 即
即![]() ,取
,取![]() 得
得![]() ,又平面
,又平面![]() 的一个法向量
的一个法向量![]() 所以
所以![]()
![]() 而二面角P-QD-A的余弦值为
而二面角P-QD-A的余弦值为![]() ,因此
,因此![]() =
=![]() 解得.m=4或者m=8(舍去)此时Q(6,4,0)设
解得.m=4或者m=8(舍去)此时Q(6,4,0)设![]() 而
而![]() =(0,-3,6)由此得点P
=(0,-3,6)由此得点P![]()
![]() 因为PQ//平面ABB1A1且平面ABB1A1的一个法向量
因为PQ//平面ABB1A1且平面ABB1A1的一个法向量![]() =(0,1,0)所以,
=(0,1,0)所以,![]() ·
·![]() =0即,
=0即,![]() 亦即得
亦即得![]() 从而P(0,4,4,)于是将四面体ADPQ视为以
从而P(0,4,4,)于是将四面体ADPQ视为以![]() ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积
ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积![]()




【考点精析】通过灵活运用向量的三角形法则和平面向量的坐标运算,掌握三角形加法法则的特点:首尾相连;三角形减法法则的特点:共起点,连终点,方向指向被减向量;坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知D=  ,给出下列四个命题:
,给出下列四个命题:
P1:(x,y)∈D,x+y+1≥0;
P2:(x,y)∈D,2x﹣y+2≤0;
P3:(x,y)∈D, ![]() ≤﹣4;
≤﹣4;
P4:(x,y)∈D,x2+y2≤2.
其中真命题的是( )
A.P1 , P2
B.P2 , P3
C.P2 , P4
D.P3 , P4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图O是等腰三角形ABC内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.
(1)(I)证明EF//BC
(2)(II)若AG等于圆O半径,且AE=MN=2![]() ,求四边形EBCF的面积
,求四边形EBCF的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)Sn为数列{an}的前n项和.已知an>0,an2+2an=4Sn+3,
(1)求{an}的通项公式;
(2)设bn=![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=![]() )
)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)在三棱住ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M , N , P分别是AB , BC , B1C1的中点,则三棱锥P-A1MN的体积是 。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=-2(x+a)lnx+x2-2ax-2a2+a,其中a>0.
(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;
(2)证明:存在a![]() (0,1),使得f(x)≥0,在区间(1,+
(0,1),使得f(x)≥0,在区间(1,+![]() )内恒成立,且f(x)=0在(1,+
)内恒成立,且f(x)=0在(1,+![]() )内有唯一解.
)内有唯一解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项的和记为Sn.如果a4=-12,a8=-4.
(1)求数列{an}的通项公式;
(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…,![]() ,…,构成一个新的数列{bn},求{bn}的前n项和
,…,构成一个新的数列{bn},求{bn}的前n项和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com