
分析 求解一元二次方程得x1,x2的值,代入$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$化简得答案.
解答 解:∵x1,x2为方程2x2-x+2=0的根,
∴$x=\frac{1±\sqrt{15}i}{4}$,
若${x}_{1}=\frac{1}{4}-\frac{\sqrt{15}}{4}i$,则${x}_{2}=\frac{1}{4}+\frac{\sqrt{15}}{4}i$,此时$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=$\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}=\frac{\frac{1}{4}+\frac{\sqrt{15}}{4}i-\frac{1}{4}+\frac{\sqrt{15}}{4}i}{(\frac{1}{4})^{2}+(\frac{\sqrt{15}}{4})^{2}}=\frac{\sqrt{15}}{2}i$;
若${x}_{1}=\frac{1}{4}+\frac{\sqrt{15}}{4}i$,则${x}_{2}=\frac{1}{4}-\frac{\sqrt{15}}{4}i$,此时$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=$\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}=\frac{\frac{1}{4}-\frac{\sqrt{15}}{4}i-\frac{1}{4}-\frac{\sqrt{15}}{4}i}{(\frac{1}{4})^{2}+(\frac{\sqrt{15}}{4})^{2}}=-\frac{\sqrt{15}}{2}i$.
故答案为:$±\frac{\sqrt{15}}{2}i$.
点评 本题考查实系数一元二次方程根的求解方法,训练了复数代数形式的乘除运算,是基础题.


科目:高中数学 来源: 题型:填空题
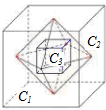 如图,记棱长为1的正方体C1,以C1各个面的中心为顶点的正八面体为C2,以C2各面的中心为顶点的正方体为C3,以C3各个面的中心为顶点的正八面体为C4,…,以此类推得一系列的多面体Cn,设Cn的棱长为an,则数列{an}的各项和为$\frac{6+3\sqrt{2}}{4}$.
如图,记棱长为1的正方体C1,以C1各个面的中心为顶点的正八面体为C2,以C2各面的中心为顶点的正方体为C3,以C3各个面的中心为顶点的正八面体为C4,…,以此类推得一系列的多面体Cn,设Cn的棱长为an,则数列{an}的各项和为$\frac{6+3\sqrt{2}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com