
(本小题满分14分)已知集合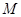 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在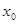 ,使得
,使得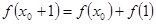 成立。
成立。
(Ⅰ)函数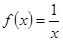 是否属于集合
是否属于集合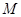 ?说明理由;
?说明理由;
(Ⅱ)设函数 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设函数 图象与函数
图象与函数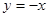 的图象有交点,
的图象有交点,
证明:函数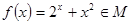 。
。
(Ⅰ)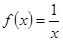
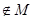 。(Ⅱ)
。(Ⅱ)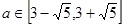 。 (Ⅲ)见解析。
。 (Ⅲ)见解析。
解析试题分析:(1)根据题意,只要sin(x0+1)=sinx0+sin1成立即可,由解析式列出方程,再由特殊角的正弦值进行证明;
(2)把解析式代入f(x+1)=f(x)+f(1),列出对应的方程,再由一元二次方程有解的条件求出k的范围,注意二次系数是否为零;
(3)根据定义只要证明f(x+1)=f(x)+f(1)有解,把解析式代入列出方程,转化为对应的函数,利用函数的零点存在性判定理进行判断..
(Ⅰ)若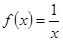
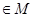 ,在定义域内存在
,在定义域内存在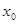 ,则
,则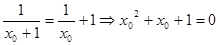 , ∵方程
, ∵方程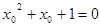 无解,∴
无解,∴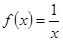
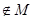 。
。
(Ⅱ)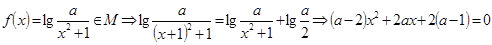 ,
,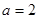 时,
时,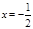 ;
;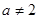 时,由
时,由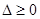 ,得
,得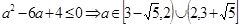 。
。
∴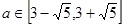 。
。
(Ⅲ)∵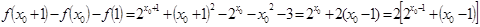 ,
,
又∵函数 图象与函数
图象与函数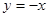 的图象有交点,设交点的横坐标为
的图象有交点,设交点的横坐标为 ,
,
则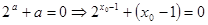 ,其中
,其中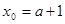 。
。
∴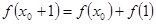 ,即
,即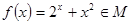 。
。
考点:对数函数图像与性质的综合应用.
点评:本题属于新定义,新情景的问题,主要利用新定义进行运算,考查了对数函数、正弦函数和指数函数的性质,函数的零点存在性判定理的应用,综合性强、难度大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本题14分)如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米,建立适当的直角坐标系,(1)求抛物线方程.(2)若将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 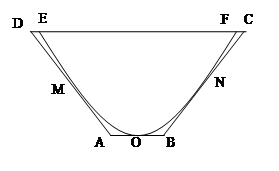
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)设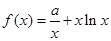 ,
,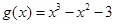 .
.
(1)当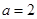 时,求曲线
时,求曲线 在
在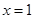 处的切线的斜率;
处的切线的斜率;
(2)如果存在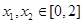 ,使得
,使得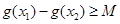 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数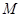 ;
;
(3)如果对于任意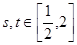 ,都有
,都有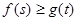 成立,求实数
成立,求实数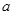 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
某市郊区一村民小组有100户农民,且都从事蔬菜种植.据调查,平均每户的年收入为3万元.为了调整产业结构,郊区政府决定动员该村部分农民从事蔬菜加工.据预测,若能动员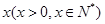 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高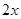 %,而从事蔬菜加工的农民平均每户的年收入将为
%,而从事蔬菜加工的农民平均每户的年收入将为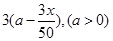 万元.
万元.
(1)在动员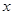 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求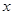 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
14分)某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,且出版的书可全部销售完. 经出版社研究决定,新书投放市场后定价为 元/本(9≤
元/本(9≤ ≤11),预计一年的销售量为
≤11),预计一年的销售量为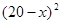 万本.
万本.
(1)求该出版社一年的利润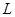 (万元)与每本书的定价
(万元)与每本书的定价 的函数关系式;
的函数关系式;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)某公司生产一种产品每年需投入固定成本为0.5万元,此外每生产100件这种产品还需要增加投入0.25万元.经预测知,当售出这种产品 百件时,若
百件时,若 ,则销售所得的收入为
,则销售所得的收入为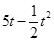 万元:若
万元:若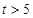 ,则销售收入为
,则销售收入为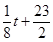 万元.
万元.
(1)若该公司的这种产品的年产量为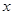 百件
百件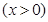 ,请把该公司生产并销售这种产品所得的年利润
,请把该公司生产并销售这种产品所得的年利润 表示为当年生产量
表示为当年生产量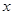 的函数;
的函数;
(2)当年产量为多少时,当年公司所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)
某市居民生活用水收费标准如下:
用水量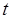 (吨) (吨) | 每吨收费标准(元) |
不超过 吨部分 吨部分 | 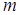 |
超过 吨不超过 吨不超过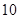 吨部分 吨部分 | 3 |
超过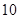 吨部分 吨部分 | 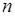 |
 吨,缴纳的水费为
吨,缴纳的水费为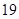 元;二月份用水量为
元;二月份用水量为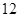 吨,缴纳的水费为
吨,缴纳的水费为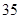 元.设某用户月用水量为
元.设某用户月用水量为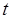 吨,交纳的水费为
吨,交纳的水费为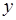 元.
元.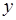 关于
关于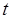 的函数关系式;
的函数关系式;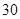 元,求该用户三月份最多可以用多少吨水?
元,求该用户三月份最多可以用多少吨水?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com