
【题目】已知圆 ![]() ,直线
,直线 ![]() .
.
(1)求直线 ![]() 所过定点
所过定点 ![]() 的坐标;
的坐标;
(2)求直线 ![]() 被圆
被圆 ![]() 所截得的弦长最短时
所截得的弦长最短时 ![]() 的值及最短弦长.
的值及最短弦长.
(3)已知点 ![]() ,在直线
,在直线 ![]() 上(
上( ![]() 为圆心),存在定点
为圆心),存在定点 ![]() (异于点
(异于点 ![]() ),满足:对于圆
),满足:对于圆 ![]() 上任一点
上任一点 ![]() ,都有
,都有 ![]() 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点 ![]() 的坐标及该常数.
的坐标及该常数.
【答案】
(1)解:依题意得, ![]() ,
,
令 ![]() ,且
,且 ![]() ,得
,得 ![]() ,
, ![]() ,∴直线
,∴直线 ![]() 过定点
过定点 ![]()
(2)解:当 ![]() 时,所截得弦长最短,由题知
时,所截得弦长最短,由题知 ![]() ,
, ![]() .
.
∴ ![]() ,得
,得 ![]() ,∴由
,∴由 ![]() 得
得 ![]() .
.
∴圆心到直线的距离为 ![]() .
.
∴最短弦长为 ![]()
(3)解:法一:由题知,直线 ![]() 的方程为
的方程为 ![]() ,假设存在定点
,假设存在定点 ![]() 满足题意,
满足题意,
则设 ![]() ,
, ![]() ,得
,得 ![]() ,且
,且 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
整理得: ![]() ,
,
∵上式对任意 ![]() 恒成立,
恒成立,
∴ ![]() 且
且 ![]() ,
,
解得 ![]() ,
, ![]() 或
或 ![]() ,
, ![]() (舍去,与
(舍去,与 ![]() 重合),
重合),
综上可知,在直线 ![]() 上存在定点
上存在定点 ![]() ,使得
,使得 ![]() 为常数
为常数 ![]() .
.
法二:设直线 ![]() 上的点
上的点 ![]() .
.
取直线 ![]() 与圆
与圆 ![]() 的交点
的交点 ![]() ,则
,则 ![]() ,
,
取直线 ![]() 与圆
与圆 ![]() 的交点
的交点 ![]() ,则
,则 ![]() ,
,
令 ![]() ,解得
,解得 ![]() 或
或 ![]() (舍去,与
(舍去,与 ![]() 重合),此时
重合),此时 ![]() ,
,
若存在这样的定点 ![]() 满足题意,则必为
满足题意,则必为 ![]() .
.
下证:点 ![]() 满足题意,
满足题意,
设圆上任意一点 ![]() ,则
,则 ![]() ,
,
∴ ![]() ∴
∴ ![]() .
.
综上可知,在直线 ![]() 上存在定点
上存在定点 ![]() ,使得
,使得 ![]() 为常数
为常数 ![]()
【解析】(1)求含字母系数的直线方程所过的定点将方程转化为该字母的等式,求得使等式恒成立时x,y的值即可;(2)利用点到直线垂线段最短的基本思路来解题;(3)先设出满足条件的点 N 的坐标及该常数,经过变形后成为求解x在闭区间上使得等式恒成立的条件.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() [cos(2x+
[cos(2x+ ![]() )+4sinxcosx]+1,x∈R.
)+4sinxcosx]+1,x∈R.
(1)求函数f(x)的最小正周期;
(2)令g(x)=af(x)+b,若函数g(x)在区间[﹣ ![]() ,
, ![]() ]上的值域为[﹣1.1],求a+b的值.
]上的值域为[﹣1.1],求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定 ![]() ,设函数
,设函数 ![]() 满足:对于任意大于
满足:对于任意大于 ![]() 的正整数
的正整数 ![]() ,
, ![]()
(1)设 ![]() ,则其中一个函数
,则其中一个函数 ![]() 在
在 ![]() 处的函数值为;
处的函数值为;
(2)设 ![]() ,且当
,且当 ![]() 时,
时, ![]() ,则不同的函数
,则不同的函数 ![]() 的个数为。
的个数为。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx,x∈(0,2π),点P(x,y)是函数f(x)图象上任一点,其中0(0,0),A(2π,0),记△OAP的面积为g(x),则g′(x)的图象可能是( )
A.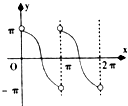
B.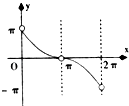
C.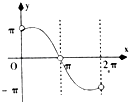
D.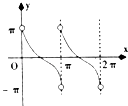
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)=f(x)+ax2﹣3x,函数g(x)的图象在点(1,g(x))处的切线平行于x轴.
(1)求a的值;
(2)求函数g(x)的极小值;
(3)设斜率为k的直线与函数f(x)的图象交于两点A(x1 , y1),B(x2 , y2),(x1<x2),证明: ![]() <k<
<k< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒中有标号分别为0,1,2,3的球各一个,这些球除标号外均相同.从盒中依次摸取两个球(每次一球,摸出后不放回),记为一次游戏.规定:摸出的两个球上的标号之和等于5为一等奖,等于4为二等奖,等于其它为三等奖.
(1)求完成一次游戏获三等奖的概率;
(2)记完成一次游戏获奖的等级为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com