分析:(Ⅰ)欲证AC
1⊥平面A
1BC,需要从平面A
1BC中找出两条相交线与AC
1垂直,由图形知,可证BC⊥AC
1,又BA
1⊥AC
1.由线面垂直的定理即可得.
(Ⅱ)求C
1到平面A
1AB的距离,本小题拟采用向量法求解,建立空间坐标系,求出平面A
1AB的法向量,以及
,求
在平面法向量上的投影即可得到点到面的距离.
(Ⅲ)求二面角A-A
1B-C的余弦值,本小题拟采用向量法求解,根据(2)求出两平面的法向量,直接求两向量夹角的余弦值的绝对值即可.
解答:
解:
(Ⅰ)证明:因为A
1在底面ABC上的射影为AC的中点D
所以平面A
1ACC
1⊥平面ABC
∵BC⊥AC且平面A
1ACC
1∩平面ABC=AC
∴BC⊥平面A
1ACC
1∴BC⊥AC
1∵AC
1⊥BA
1且BC
1∩BA
1=B
∴AC
1⊥平面A
1BC
(Ⅱ)如图所示,以C为坐标原点建立空间直角坐标系
∵AC
1⊥平面A
1BC∴AC
1⊥A
1C
∴四边形A
1ACC
1是菱形∵D是AC的中点
∴∠A
1AD=60°∴A(2,0,0)A
1(1,0,
)
B(0,2,0)C
1(-1,0,
)
∴
=(1,0,
)
=(-2,2,0)
设平面A
1AB的法向量
=(x,y,z),则
,令z=1,
∴
=(
,
,1)
∵
=(2,0,0)∴
d==∴C
1到平面A
1AB的距离为
(Ⅲ)平面A
1AB的法向量
=(
,
,1),平面A
1BC的法向量
=(-3,0,
)
∴
cos<,>==-,
设二面角A-A
1B-C的平面角为θ,θ为锐角,
∴
cosθ=即二面角A-A
1B-C的余弦值为
点评:本题考查线面垂直的证明,点到面距离的求法,二面角的求法,由解题过程可以看出,用向量法求点到面的距离,求二面角是一个很实用的方法,解题中要善于运用,在求解此类题时,求面的法向量是一个重点,要学会怎么赋值.

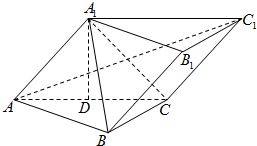 已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.
已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1. 解:
解:

 已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形,∠B1BC=60°,侧面BB1C1C⊥底面ABC,∠ABC=90°,二面角A-B1B-C为30°.
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形,∠B1BC=60°,侧面BB1C1C⊥底面ABC,∠ABC=90°,二面角A-B1B-C为30°. 已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直,BB1=BC,∠B1BC=60°,AB=AC,M是B1C1的中点.
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直,BB1=BC,∠B1BC=60°,AB=AC,M是B1C1的中点. 如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 已知斜三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC,A1B⊥ACl
已知斜三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC,A1B⊥ACl