
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:函数
满足:函数![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时
时![]() 是函数
是函数![]() 的导函数)成立.若
的导函数)成立.若![]() ,则
,则![]() 的大小关系是
的大小关系是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】![]() 函数
函数![]() 的图象关于直线
的图象关于直线![]() 对称,向左平移一个单位后得到函数
对称,向左平移一个单位后得到函数![]() 的图象,
的图象, ![]() 关于
关于![]() 轴对称,
轴对称, ![]() 为偶函数,
为偶函数, ![]() 函数
函数![]() 为奇函数,
为奇函数, ![]() ,
, ![]() 当
当![]() 时,
时, ![]() ,
, ![]() 函数
函数![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,函数
时,函数![]() 上单调递减,
上单调递减, ![]() ,
, ![]() ,
,
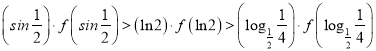 ,即
,即![]() ,故选A.
,故选A.
【方法点睛】本题主要考察抽象函数的单调性以及函数的求导法则,属于难题.求解这类问题一定要耐心读题、读懂题,通过对问题的条件和结论进行类比、联想、抽象、概括,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点也是难点就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.本题通过观察四个选项,联想到函数![]() ,再结合条件判断出其单调性,进而得出正确结论.
,再结合条件判断出其单调性,进而得出正确结论.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
(Ⅰ) 求证:PC⊥AD;
(Ⅱ) 在棱PB上是否存在一点Q,使得A,Q,M,D四点共面?若存在,指出点Q的位置并证明;若不存在,请说明理由;
(Ⅲ) 求点D到平面PAM的距离. 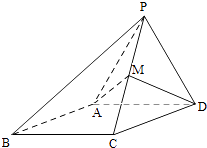
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() .在以原点为极点,
.在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如: 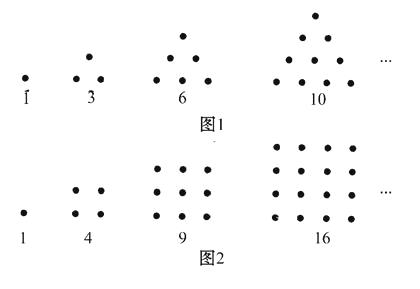
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…,这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
A.289
B.1024
C.1225
D.1378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=n2﹣n,数列{bn}的前n项和Tn=4﹣bn .
(1)求数列{an}和{bn}的通项公式;
(2)设cn= ![]() anbn , 求数列{cn}的前n项和Rn的表达式.
anbn , 求数列{cn}的前n项和Rn的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.
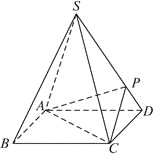
(1)求证:![]() .
.
(2)若![]() ⊥平面
⊥平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com