
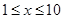 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是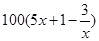 元.
元.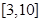 ;(2)以每小时6千克的速度能获得最大利润,最大利润为457500元.
;(2)以每小时6千克的速度能获得最大利润,最大利润为457500元.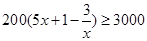 ,这个不等式的解就是所求范围.(2)求利润最大问题,一般是列出函数式,再借助函数的知识解决,本题就是把利润
,这个不等式的解就是所求范围.(2)求利润最大问题,一般是列出函数式,再借助函数的知识解决,本题就是把利润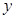 表示为生产速度
表示为生产速度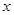 的函数
的函数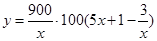 ,这个函数可以看作为关于
,这个函数可以看作为关于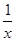 的二次函数,从而可以利用二次函数的知识得解.
的二次函数,从而可以利用二次函数的知识得解.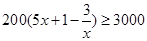
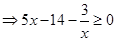 4分
4分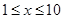 ,可解得
,可解得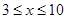 6分
6分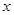 的取值范围是
的取值范围是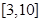 7分
7分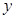 元,则
元,则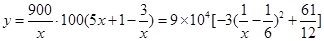 11分
11分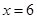 时,
时,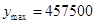 元. 13分
元. 13分 14分
14分

科目:高中数学 来源:不详 题型:解答题
 R).
R). )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围;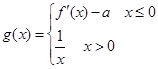 ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值;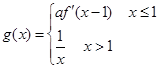 ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
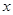 (单位:元,
(单位:元,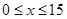 )的关系是t=
)的关系是t=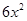 .
.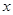 的函数;
的函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
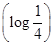 ·f
·f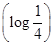 ,则a,b,c的大小关系是( ).
,则a,b,c的大小关系是( ).| A.a>b>c | B.b>a>c |
| C.c>a>b | D.a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com