
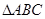 是边长为2的正三角形,
是边长为2的正三角形,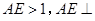 平面ABC,平面
平面ABC,平面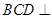 平面ABC,BD=CD,且
平面ABC,BD=CD,且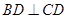 .
.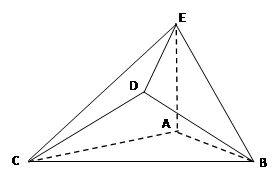
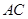 ∥
∥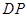 ,又
,又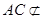 平面
平面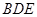 ,
,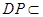 平面
平面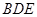 ,从而得到证明。
,从而得到证明。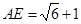
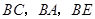 的中点
的中点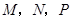 ,连接
,连接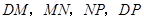 ,则
,则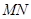 ∥
∥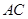 ,
,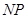 ∥
∥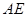 ,且
,且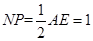 ,
,
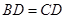 ,
,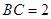 ,
,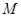 为
为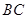 的中点,
的中点,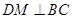 ,
,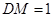 ,
,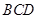 ⊥平面
⊥平面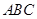 ,
,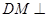 平面
平面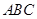 . 3分
. 3分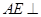 平面
平面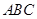 ,
,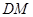 ∥
∥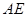 , 5分
, 5分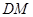 ∥
∥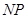 ,且
,且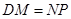 ,因此四边形
,因此四边形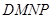 为平行四边形,
为平行四边形,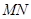 ∥
∥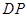 ,所以
,所以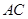 ∥
∥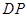 ,又
,又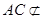 平面
平面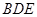 ,
,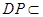 平面
平面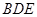 ,
,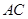 ∥平面
∥平面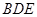 . 7分
. 7分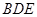 的法向量
的法向量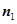 ,计算
,计算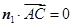 即证)
即证)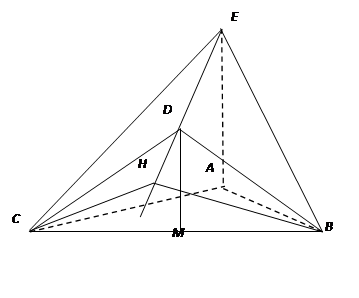
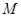 作
作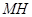 垂直
垂直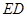 的延长线于
的延长线于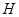 ,连接
,连接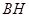 .
.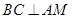 ,
,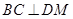 ,
,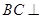 平面
平面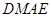 ,
,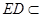 平面
平面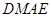
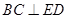 .
.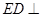 平面
平面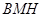 ,
,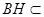 平面
平面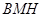 ,
,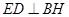 .
.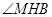 为二面角
为二面角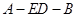 的平面角,
的平面角,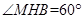 . 10分
. 10分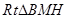 中,
中,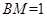 ,则
,则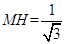 ,
,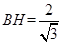 .
.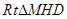 中,
中,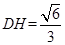 .
.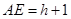 ,则
,则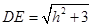 ,所以
,所以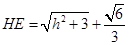 ,又
,又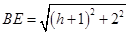
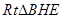 中,
中,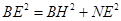 ,即
,即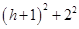 =
=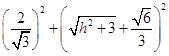 ,
,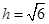 ,所以
,所以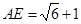 . 14分
. 14分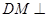 平面
平面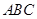 ,
,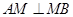 ,
,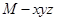 .
.
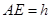 ,则
,则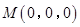 ,
,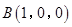 ,
,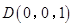
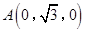 ,
,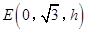 ,
,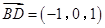 ,
,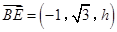 .
.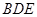 的法向量
的法向量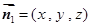
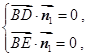 所以
所以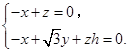
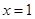 , 所以
, 所以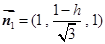 ,11分
,11分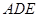 的法向量
的法向量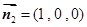 ,
,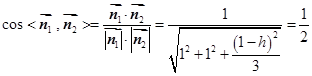 ,
,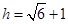 , 即
, 即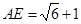 . 14分
. 14分

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com