在平面直角坐标系内,动圆C过定点F(1,0),且与定直线x=-1相切.
(1)求动圆圆心C的轨迹C2的方程;
(2)中心在O的椭圆C1的一个焦点为F,直线l过点M(4,0).若坐标原点O关于直线l的对称点P在曲线C2上,且直线l与椭圆C1有公共点,求椭圆C1的长轴长取得最小值时的椭圆方程.
解:(1)由题意,可得
∵圆心C到定点F(1,0)的距离与到定直线x=-1的距离相等

∴由抛物线定义知,C的轨迹C
2是以F(1,0)为焦点,
直线x=-1为准线的抛物线
∴动圆圆心C的轨迹C
2的方程为y
2=4x.
(2)设P(m,n),直线l方程为y=k(x-4),则OP中点为(

,

),
∵O、P两点关于直线y=k(x-4)对称,
∴

,即

,解之得

将其代入抛物线方程,得:(-

)
2=4×

,解之得k
2=1.
设椭圆C
1的方程为

,
联列

,消去y得:(a
2+b
2)x
2-8a
2x+16a
2-a
2b
2=0
由△=(-8a
2)
2-4(a
2+b
2)(16a
2-a
2b
2)≥0,得a
2+b
2≥16,
注意到b
2=a
2-1,即2a
2≥17,可得a≥
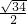
,即2a

,
因此,椭圆C
1长轴长的最小值为

,此时椭圆的方程为

.
分析:(1)根据抛物线的定义,动圆圆心C的轨迹是以F(1,0)为焦点,x=-1为准线的抛物线,结合抛物线的基本概念即可求出C的轨迹C
2的方程;
(2)设P(m,n),直线l方程为y=k(x-4),根据OP被l垂直平分建立关于k、m、n的方程组,解之可得m=

且n=-

.将P的坐标关于k的形式代入抛物线方程,解之得k
2=1,从而得到直线l的方程.然后根据直线l与椭圆C
1有公共点,两方程联解并运用根的判别式解出a
2+b
2≥16,结合b
2=a
2-1可得a的最小值为
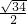
,由此即可得到椭圆C
1的长轴长取得最小值时的椭圆方程.
点评:本题给出动点P满足的条件,求P的轨迹方程并依此求椭圆C
1的长轴长取得最小值时的椭圆方程.着重考查了抛物线、椭圆的标准方程与简单几何性质、一元二次方程根与系数的关系和直线与圆锥曲线的位置关系等知识点,属于中档题.


 ,
, ),
), ,即
,即 ,解之得
,解之得
 )2=4×
)2=4× ,解之得k2=1.
,解之得k2=1. ,
, ,消去y得:(a2+b2)x2-8a2x+16a2-a2b2=0
,消去y得:(a2+b2)x2-8a2x+16a2-a2b2=0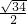 ,即2a
,即2a ,
, ,此时椭圆的方程为
,此时椭圆的方程为 .
. 且n=-
且n=- .将P的坐标关于k的形式代入抛物线方程,解之得k2=1,从而得到直线l的方程.然后根据直线l与椭圆C1有公共点,两方程联解并运用根的判别式解出a2+b2≥16,结合b2=a2-1可得a的最小值为
.将P的坐标关于k的形式代入抛物线方程,解之得k2=1,从而得到直线l的方程.然后根据直线l与椭圆C1有公共点,两方程联解并运用根的判别式解出a2+b2≥16,结合b2=a2-1可得a的最小值为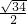 ,由此即可得到椭圆C1的长轴长取得最小值时的椭圆方程.
,由此即可得到椭圆C1的长轴长取得最小值时的椭圆方程.

 设定义域为R的函数f(x)=
设定义域为R的函数f(x)=