Question

【题目】某绿色有机水果店中一款有机草莓味道鲜甜，店家每天以每斤元的价格从农场购进适量草莓，然后以每斤元的价格出售，如果当天卖不完，剩下的草莓由果汁厂以每斤元的价格回收.

（1）若水果店一天购进斤草莓，求当天的利润（单位：元）关于当天需求量（单位：斤，）的函数解析式；

（2）水果店记录了天草莓的日需求量（单位：斤），整理得下表：

日需求量	14	15	16	17	18	19	20
频数	14	22	14	16	15	13	6

①假设水果店在这天内每天购进斤草莓，求这天的日利润（单位：元）的平均数；

②若水果店一天购进斤草莓，以天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于元的概率.

Answer 1

【答案】（1）；（2）①，②0.64

【解析】

（1）对需求量n进行分类，时，进货有剩余，利润；时，进货能全部出清，利润.

（2）根据不同的需求量，求出各自的利润，再求平均数.由利润不少于元，求得需求量的范围，结合频数可求概率.

（1）当日需求量时，利润；

当日需求量时，利润.

所以当天的利润关于当天需求量的函数解析式为

（2）①假设水果店在这天内每天购进斤草莓，则：

日需求量为斤时，利润；日需求量为斤时，利润；

日需求量为斤时，利润；日需求量不小于时，利润.

故这天的日利润（单位：元）的平均数为：

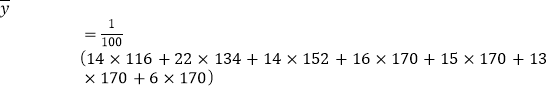，解得（元）.

②利润不低于元时，当日需求量当且仅当不少于斤.以频率预估概率，

得当天的利润不少于元的概率为.