
【题目】已知![]() 在椭圆
在椭圆![]() 上,
上,![]() 为右焦点,
为右焦点,![]() 轴,
轴,![]() 为椭圆上的四个动点,且
为椭圆上的四个动点,且![]() ,
,![]() 交于原点
交于原点![]() .
.
(1)判断直线![]() 与椭圆的位置关系;
与椭圆的位置关系;
(2设![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 的值是否为定值,若是,请求出此定值,并求出四边形
的值是否为定值,若是,请求出此定值,并求出四边形![]() 面积的最大值,否则说明理由.
面积的最大值,否则说明理由.
【答案】(1)直线![]() 与椭圆相切或相交.(2)
与椭圆相切或相交.(2)![]() 的值是定值,
的值是定值,![]() ;
;![]()
【解析】
(1)将直线![]() 变形,可确定直线
变形,可确定直线![]() 所过定点的坐标,可得该定点坐标在椭圆上,即可判断出直线
所过定点的坐标,可得该定点坐标在椭圆上,即可判断出直线![]() 与椭圆的位置关系.
与椭圆的位置关系.
(2)先根据条件,求得椭圆的标准方程.讨论直线![]() 的斜率情况可知当斜率不存在或斜率为0时不满足
的斜率情况可知当斜率不存在或斜率为0时不满足![]() .进而设直线
.进而设直线![]() 的方程为
的方程为![]() ,联立椭圆方程,利用韦达定理及等式
,联立椭圆方程,利用韦达定理及等式![]() ,化简即可求得
,化简即可求得![]() 的值,确定
的值,确定![]() 为定值;由点到直线距离公式求得
为定值;由点到直线距离公式求得![]() ,利用弦长公式求得
,利用弦长公式求得![]() ,即可用
,即可用![]() 表示出
表示出![]() ,由二次函数性质求得
,由二次函数性质求得![]() 的最大值,并根据
的最大值,并根据![]() 即可求得
即可求得![]() 的最大值.
的最大值.
(1)直线![]() ,
,
将直线方程化简变形可得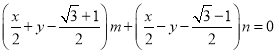 ,
,
因为![]() ,令
,令 ,解得
,解得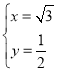 ,
,
所以直线![]() 过定点
过定点![]() ,
,
而由![]() 在椭圆上,可知直线
在椭圆上,可知直线![]() 与椭圆相切或相交.
与椭圆相切或相交.
(2)![]() 在椭圆
在椭圆![]() 上,
上,![]() 轴,
轴,
由椭圆性质可得![]() ,
,
则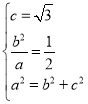 解得
解得![]() ,
,
所以椭圆的标准方程为![]() ,
,
因为![]() ,
,![]() ,
,![]() 为椭圆上的四个动点且
为椭圆上的四个动点且![]() ,
,![]() 交于原点
交于原点![]() .
.
所以![]() ,
,![]() ,
,
当直线![]() 的斜率不存在时,不满足
的斜率不存在时,不满足![]() ,因而直线
,因而直线![]() 的斜率一定存在.
的斜率一定存在.
当直线![]() 斜率存在且为0时,不满足
斜率存在且为0时,不满足![]() ,所以直线
,所以直线![]() 的斜率一定存在且不为0.
的斜率一定存在且不为0.
设直线![]() 的方程为
的方程为![]() .
.
则 ,化简可得
,化简可得![]() ,
,
所以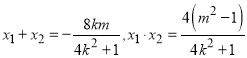 ,
,
![]()
因为![]() ,
,
所以![]() ,
,
则 ,
,
整理可得![]() ,
,
解得![]() .
.
由题意可知![]() 的位置等价,所以不妨设
的位置等价,所以不妨设![]() ,则
,则![]() ,
,
则![]() ,
,
即![]() 为定值.
为定值.
直线![]() 的方程为
的方程为![]() .即
.即![]()
则点![]() 到直线
到直线![]() 的距离为
的距离为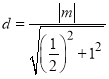
因为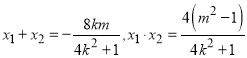
代入可得![]()
则由弦长公式可得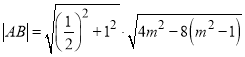
所以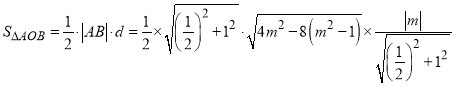
![]()
![]()
![]()
当![]() 时取等号.而
时取等号.而![]() 时满足
时满足![]() .
.
所以![]()
此时![]()
故四边形![]() 面积的最大值的最大值为4
面积的最大值的最大值为4


科目:高中数学 来源: 题型:
【题目】某城市的甲区、乙区分别对6个企业进行评估,综合得分情况如茎叶图所示.
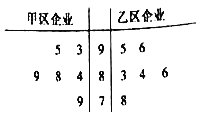
(1)根据茎叶图,分别求甲、乙两区引进企业得分的平均值;
(2)规定85分以上(含85分)为优秀企业,若从甲、乙两个区准备引进的优秀企业中各随机选取一个,求这两个企业得分的差的绝对值不超过5分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱![]() 的底面边长为2,侧棱
的底面边长为2,侧棱![]() ,
,![]() 为上底面
为上底面![]() 上的动点,给出下列四个结论中正确结论为( )
上的动点,给出下列四个结论中正确结论为( )
A.若![]() ,则满足条件的
,则满足条件的![]() 点有且只有一个
点有且只有一个
B.若![]() ,则点
,则点![]() 的轨迹是一段圆弧
的轨迹是一段圆弧
C.若![]() ∥平面
∥平面![]() ,则
,则![]() 长的最小值为2
长的最小值为2
D.若![]() ∥平面
∥平面![]() ,且
,且![]() ,则平面
,则平面![]() 截正四棱柱
截正四棱柱![]() 的外接球所得平面图形的面积为
的外接球所得平面图形的面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解数学课外兴趣小组的学习情况,从某次测试的成绩中随机抽取![]() 名学生的成绩进行分析,得到如图所示的频率分布直方图.
名学生的成绩进行分析,得到如图所示的频率分布直方图.

(1)根据频率分布直方图估计本次测试成绩的众数;
(2)从成绩不低于![]() 分的两组学生中任选
分的两组学生中任选![]() 人,求选出的两人来自同一组的概率.
人,求选出的两人来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. 288种 B. 144种 C. 720种 D. 360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为![]() :1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4纸的长度为( )
,那么A4纸的长度为( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信红包是一款可以实现收发红包、查收记录和提现的手机应用.某网络运营商对甲、乙两个品牌各5种型号的手机在相同环境下抢到的红包个数进行统计,得到如表数据:
手机品牌 |
|
|
|
|
|
甲品牌(个 | 4 | 3 | 8 | 6 | 12 |
乙品牌(个 | 5 | 7 | 9 | 4 | 3 |
手机品牌 | 优 | 非优 | 合计 |
| |||
乙品牌(个 | |||
合计 |
(1)如果抢到红包个数超过5个的手机型号为“优”,否则“非优”,请完成上述![]() 列联表,据此判断是否有
列联表,据此判断是否有![]() 的把握认为抢到的红包个数与手机品牌有关?
的把握认为抢到的红包个数与手机品牌有关?
(2)如果不考虑其它因素,要从甲品牌的5种型号中选出3种型号的手机进行大规模宣传销售.以![]() 表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量
表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | <>2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]()
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》的盈不足章第19个问题中提到:“今有良马与驽马发长安,至齐.齐去长安三千里.良马初日行一百九十三里,日增一十三里.驽马初日行九十七里,日减半里…”其大意为:“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里.良马第一天行193里,之后每天比前一天多行13里.驽马第一天行97里,之后每天比前一天少行0.5里…”试问前4天,良马和驽马共走过的路程之和的里数为( )

A.1235B.1800C.2600D.3000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com