
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЕФгЏВЛзуеТЕк19ИіЮЪЬтжаЬсЕНЃКЁАНёгаСМТэгыцхТэЗЂГЄАВЃЌжСЦыЃЎЦыШЅГЄАВШ§ЧЇРяЃЎСМТэГѕШеаавЛАйОХЪЎШ§РяЃЌШедівЛЪЎШ§РяЃЎцхТэГѕШеааОХЪЎЦпРяЃЌШеМѕАыРяЁЁБЦфДѓвтЮЊЃКЁАЯждкгаСМТэКЭцхТэЭЌЪБДгГЄАВГіЗЂЕНЦыШЅЃЎвбжЊГЄАВКЭЦыЕФОрРыЪЧ3000РяЃЎСМТэЕквЛЬьаа193РяЃЌжЎКѓУПЬьБШЧАвЛЬьЖраа13РяЃЎцхТэЕквЛЬьаа97РяЃЌжЎКѓУПЬьБШЧАвЛЬьЩйаа0.5РяЁЁБЪдЮЪЧА4ЬьЃЌСМТэКЭцхТэЙВзпЙ§ЕФТЗГЬжЎКЭЕФРяЪ§ЮЊЃЈЁЁ ЁЁЃЉ

A.1235B.1800C.2600D.3000
ЁОД№АИЁПA
ЁОНтЮіЁП
ИљОнЬтвтСМТэУПЬьТЗГЬЙЙГЩвд![]() ЮЊЪзЯюЃЌ
ЮЊЪзЯюЃЌ![]() ЮЊЙЋВюЕФЕШВюЪ§СаЃЌцхТэУПЬьТЗГЬЙЙГЩвд
ЮЊЙЋВюЕФЕШВюЪ§СаЃЌцхТэУПЬьТЗГЬЙЙГЩвд![]() ЮЊЪзЯюЃЌ
ЮЊЪзЯюЃЌ![]() ЮЊЙЋВюЕФЕШВюЪ§СаЃЌЙЪРћгУЕШВюЪ§СаЕФЧѓКЭЙЋЪНПЩжБНгЧѓЕУНсЙћЃЎ
ЮЊЙЋВюЕФЕШВюЪ§СаЃЌЙЪРћгУЕШВюЪ§СаЕФЧѓКЭЙЋЪНПЩжБНгЧѓЕУНсЙћЃЎ
вђЮЊГЄАВКЭЦыЕФОрРыЪЧ3000РяЃЎСМТэЕквЛЬьаа193РяЃЌжЎКѓУПЬьБШЧАвЛЬьЖраа13РяЃЎ
цхТэЕквЛЬьаа97РяЃЌжЎКѓУПЬьБШЧАвЛЬьЩйаа0.5РяЃЌ
ЫљвдЧА4ЬьЃЌСМТэКЭцхТэЙВзпЙ§ЕФТЗГЬжЎКЭЕФРяЪ§ЮЊЃК
![]() ЃЎ
ЃЎ
ЙЪбЁЃКAЃЎ


 зївЕИЈЕМЯЕСаД№АИ
зївЕИЈЕМЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() дкЭждВ
дкЭждВ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЮЊгвНЙЕуЃЌ
ЮЊгвНЙЕуЃЌ![]() жсЃЌ
жсЃЌ![]() ЮЊЭждВЩЯЕФЫФИіЖЏЕуЃЌЧв
ЮЊЭждВЩЯЕФЫФИіЖЏЕуЃЌЧв![]() ЃЌ
ЃЌ![]() НЛгкдЕу
НЛгкдЕу![]() .
.
ЃЈ1ЃЉХаЖЯжБЯп![]() гыЭждВЕФЮЛжУЙиЯЕЃЛ
гыЭждВЕФЮЛжУЙиЯЕЃЛ
ЃЈ2Щш![]() ЃЌ
ЃЌ![]() Тњзу
Тњзу![]() ЃЌХаЖЯ
ЃЌХаЖЯ![]() ЕФжЕЪЧЗёЮЊЖЈжЕЃЌШєЪЧЃЌЧыЧѓГіДЫЖЈжЕЃЌВЂЧѓГіЫФБпаЮ
ЕФжЕЪЧЗёЮЊЖЈжЕЃЌШєЪЧЃЌЧыЧѓГіДЫЖЈжЕЃЌВЂЧѓГіЫФБпаЮ![]() УцЛ§ЕФзюДѓжЕЃЌЗёдђЫЕУїРэгЩ.
УцЛ§ЕФзюДѓжЕЃЌЗёдђЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдЦНУцжБНЧзјБъЯЕ
ЮЊВЮЪ§ЃЉЃЌвдЦНУцжБНЧзјБъЯЕ![]() ЕФдЕу
ЕФдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЭждВ
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЭждВ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓжБЯп![]() ЕФЦеЭЈЗНГЬЃЈаДГЩвЛАуЪНЃЉКЭЭждВ
ЕФЦеЭЈЗНГЬЃЈаДГЩвЛАуЪНЃЉКЭЭждВ![]() ЕФжБНЧзјБъЗНГЬЃЈаДГЩБъзМЗНГЬЃЉЃЛ
ЕФжБНЧзјБъЗНГЬЃЈаДГЩБъзМЗНГЬЃЉЃЛ
ЃЈ2ЃЉШєжБЯп![]() гыЭждВ
гыЭждВ![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧвгы
СНЕуЃЌЧвгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвддЕуOЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЧњЯпCЕФЦеЭЈЗНГЬЃЛ
ЃЈ2ЃЉжБЯпlЕФВЮЪ§ЗНГЬЮЊ![]() ЃЌЃЈtЮЊВЮЪ§ЃЉЃЌжБЯпlгыxжсНЛгкЕуFЃЌгыЧњЯпCЕФНЛЕуЮЊAЃЌBЃЌЕБ
ЃЌЃЈtЮЊВЮЪ§ЃЉЃЌжБЯпlгыxжсНЛгкЕуFЃЌгыЧњЯпCЕФНЛЕуЮЊAЃЌBЃЌЕБ![]() ШЁзюаЁжЕЪБЃЌЧѓжБЯпlЕФжБНЧзјБъЗНГЬЃЎ
ШЁзюаЁжЕЪБЃЌЧѓжБЯпlЕФжБНЧзјБъЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЖўУцНЧ
ЃЌЖўУцНЧ![]() ЮЊ
ЮЊ![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌжБЯп
ЃЌжБЯп![]() ЮЊЧњЯп
ЮЊЧњЯп![]() ЕФЧаЯпЃЈ
ЕФЧаЯпЃЈ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЎ
ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉгУ![]() БэЪО
БэЪО![]() жаЕФзюаЁжЕЃЌЩшКЏЪ§
жаЕФзюаЁжЕЃЌЩшКЏЪ§![]() ЃЌШєКЏЪ§
ЃЌШєКЏЪ§
![]() ЮЊдіКЏЪ§ЃЌЧѓЪЕЪ§
ЮЊдіКЏЪ§ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЬнаЮABCDжаЃЌADЁЮBCЃЌABЃНBC![]() 2ЃЌEЮЊADЕФжаЕуЃЌOЪЧACгыBEЕФНЛЕуЃЌНЋЁїABEбиBEЗелЕНЭМ2жаЁїA1BEЕФЮЛжУЕУЕНЫФРтзЖA1ЉBCDEЃЎ
2ЃЌEЮЊADЕФжаЕуЃЌOЪЧACгыBEЕФНЛЕуЃЌНЋЁїABEбиBEЗелЕНЭМ2жаЁїA1BEЕФЮЛжУЕУЕНЫФРтзЖA1ЉBCDEЃЎ
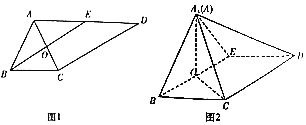
ЃЈ1ЃЉЧѓжЄЃКCDЁЭA1CЃЛ
ЃЈ2ЃЉШєA1C![]() ЃЌBEЃН2
ЃЌBEЃН2![]() ЃЌЧѓЕуCЕНЦНУцA1EDЕФОрРыЃЎ
ЃЌЧѓЕуCЕНЦНУцA1EDЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ТњзуЃК
ТњзуЃК![]() ЃЈГЃЪ§
ЃЈГЃЪ§![]() ЃЉЃЌ
ЃЉЃЌ![]()
![]() .Ъ§Са
.Ъ§Са![]() ТњзуЃК
ТњзуЃК![]()
![]() .
.
ЃЈ1ЃЉЧѓ![]()
![]()
![]()
![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓГіЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ3ЃЉЮЪЃКЪ§Са![]() ЕФУПвЛЯюФмЗёОљЮЊећЪ§ЃПШєФмЃЌЧѓГіkЕФЫљгаПЩФмжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩ.
ЕФУПвЛЯюФмЗёОљЮЊећЪ§ЃПШєФмЃЌЧѓГіkЕФЫљгаПЩФмжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаЫФИіНсТлЃЌЦфжае§ШЗЕФЪЧ( )
ЂйДгдШЫйДЋЫЭЕФЩњВњСїЫЎЯпЩЯЃЌУП30ЗжжгГщШЁвЛМўВњЦЗНјааМьВтЃЌетбљЕФГщбљЪЧЗжВуГщбљЃЛЂкЁА![]() ЁБГЩСЂЕФБивЊЖјВЛГфЗжЬѕМўЪЧЁА
ЁБГЩСЂЕФБивЊЖјВЛГфЗжЬѕМўЪЧЁА![]() ЁБЃЛЂлШєбљБОЪ§Он
ЁБЃЛЂлШєбљБОЪ§Он![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЕФБъзМВюЮЊ3ЃЌдђ
ЕФБъзМВюЮЊ3ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЕФЗНВюЮЊ145ЃЛЂм
ЕФЗНВюЮЊ145ЃЛЂм![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЯђСПЃЌдђгЩЁА
ЪЧЯђСПЃЌдђгЩЁА![]() ЁБРрБШЕУЕНЁА
ЁБРрБШЕУЕНЁА![]() ЁБЕФНсТлЪЧе§ШЗЕФ.
ЁБЕФНсТлЪЧе§ШЗЕФ.
A.ЂйЂмB.ЂкЂлC.ЂйЂлD.ЂкЂм
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com