
已知函数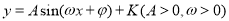 的最大值为4,最小值为0,最小正周期为
的最大值为4,最小值为0,最小正周期为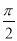 ,直线
,直线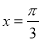 是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
A.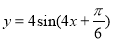 B.
B.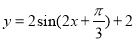
C.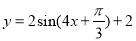 D.
D.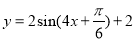
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016届江西省高一下学期期末考试数学试卷(解析版) 题型:填空题
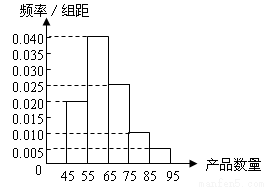
为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在[55,75)的人数是 .
查看答案和解析>>
科目:高中数学 来源:2016届江西省九江七校高一下学期期中联考数学试卷(解析版) 题型:选择题
下列结论中,正确结论的个数是( )
(1)若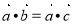 ,且
,且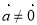 ,则
,则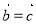
(2)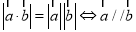
(3)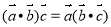
(4)若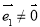 ,
,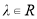 ,
,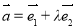 ,
,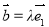 ,
,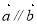 则
则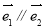 或
或
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期期末考试数学试卷(解析版) 题型:解答题
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),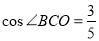 .以
.以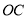 所在直线为
所在直线为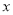 轴,以
轴,以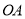 所在直线为
所在直线为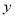 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求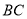 所在直线的方程及新桥BC的长;
所在直线的方程及新桥BC的长;
(Ⅱ)当OM多长时,圆形保护区的面积最大?
并求此时圆的方程.
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期期末考试理科数学试卷(解析版) 题型:解答题
已知等差数列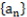 满足:
满足: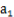 =2,且
=2,且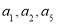 成等比数列.
成等比数列.
(1)求数列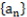 的通项公式.
的通项公式.
(2)记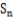 为数列
为数列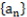 的前n项和,是否存在正整数n,使得
的前n项和,是否存在正整数n,使得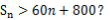 若存在,求n的最小值;若不存在,说明理由.
若存在,求n的最小值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com