
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),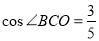 .以
.以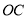 所在直线为
所在直线为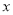 轴,以
轴,以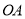 所在直线为
所在直线为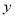 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求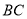 所在直线的方程及新桥BC的长;
所在直线的方程及新桥BC的长;
(Ⅱ)当OM多长时,圆形保护区的面积最大?
并求此时圆的方程.
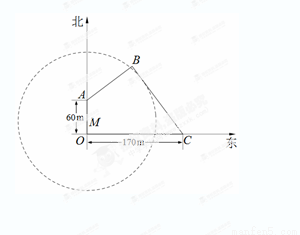
(1)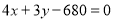 ,
,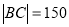 ;(2)线段
;(2)线段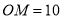 米时,圆形保护区最大;方程为
米时,圆形保护区最大;方程为
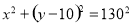
【解析】
试题分析:(1)在求直线方程时,应先选择恰当的直线方程的形式,并注意各种形式的适用条件,用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直的直线或经过原点的直线,故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况;(2)根据圆的圆心坐标和半径求圆的标准方程.(3)判断直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,用几何法;若方程中含参数,或圆心到直线的距离的表达较繁琐,则用代数法.
试题解析:(Ⅰ)建立平面直角坐标系xOy.
由条件知A(0, 60),C(170, 0),
直线BC的斜率k BC=-tan∠BCO=-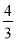 .
.
又因为AB⊥BC,所以直线AB的斜率k AB=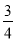
设点B的坐标为(a,b),则k BC=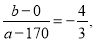
k AB=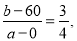
解得a=80,b=120.所以BC=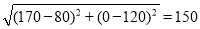 .
.
因此直线BC的方程为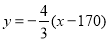 ,即
,即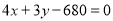 ..............6分
..............6分
新桥BC的长是150 m.
(Ⅱ)设保护区的边界圆M的半径为r m,OM=d m,(0≤d≤60).
由知,直线BC的方程为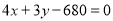
由于圆M与直线BC相切,故点M(0,d)到直线BC的距离是r,
即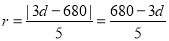 .
.
因为O和A到圆M上任意一点的距离均不少于80 m,
所以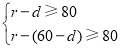 即
即 解得
解得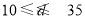
故当d=10时, 最大,即圆面积最大.
最大,即圆面积最大.
所以当OM = 10 m时,圆形保护区的面积最大.此时圆的方程为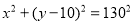 ..........................13分
..........................13分
考点:(1)直线方程的应用;(2)直线与圆的方程的综合应用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:2016届江西省高一下学期期末考试数学试卷(解析版) 题型:选择题
某班有48名学生,在一次考试中统计出平均分为70分,方差为75,后来发现有2名同学的分数登错了,甲实得80分却记了50分,乙得70分却记了100分,更正后平均分和方差分别是( )
A.70,75 B.70,50 C.70.1.04 D.65,25
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期第一次月考数学试卷(解析版) 题型:选择题
把曲线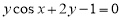 先沿
先沿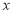 轴向右平移
轴向右平移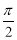 个单位,再沿
个单位,再沿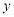 轴向下平移1个单位,得到的曲线方程为( )
轴向下平移1个单位,得到的曲线方程为( )
A.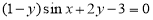 B.
B.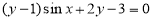
C.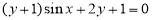 D.
D.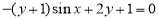
查看答案和解析>>
科目:高中数学 来源:2016届江西省九江七校高一下学期期中联考数学试卷(解析版) 题型:选择题
已知函数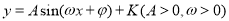 的最大值为4,最小值为0,最小正周期为
的最大值为4,最小值为0,最小正周期为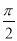 ,直线
,直线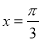 是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
A.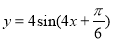 B.
B.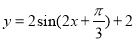
C.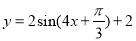 D.
D.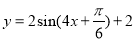
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期期末考试理科数学试卷(解析版) 题型:填空题
在△ABC中,设AD为BC边上的高,且AD ? BC,b,c分别表示角B,C所对的边长,则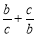 的取值范围是____________.
的取值范围是____________.
查看答案和解析>>
科目:高中数学 来源:2016届江苏连云港新海高级中学高一下学期期中考试数学试卷(解析版) 题型:解答题
已知向量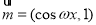 ,
,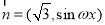 (
(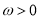 ),函数
),函数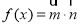 ,且
,且 图象上一个最高点为
图象上一个最高点为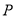
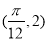 ,与
,与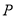 最近的一个最低点的坐标为
最近的一个最低点的坐标为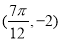 .
.
(1)求函数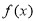 的解析式;
的解析式;
(2)设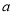 为常数,判断方程
为常数,判断方程 在区间
在区间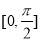 上的解的个数;
上的解的个数;
(3)在锐角 中,若
中,若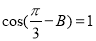 ,求
,求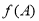 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com