
【题目】在函数定义域内,若存在区间![]() ,使得函数值域为
,使得函数值域为![]() ,则称此函数为“
,则称此函数为“![]() 档类正方形函数”,已知函数
档类正方形函数”,已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 的最大值是1,求实数
的最大值是1,求实数![]() 的值;
的值;
(3)当![]() 时,是否存在
时,是否存在![]() ,使得函数
,使得函数![]() 为“1档类正方形函数”?若存在,求出实数
为“1档类正方形函数”?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)根据指数函数的性质和对数函数想性质可得到函数![]() 的值域;
的值域;
(2)利用换元法设![]() ,然后对参数
,然后对参数![]() 进行分类讨论,分
进行分类讨论,分![]() 和
和![]() 两种情况进行讨论函数
两种情况进行讨论函数![]() 的最大值,根据最大值取得的情况计算出
的最大值,根据最大值取得的情况计算出![]() 的取值;
的取值;
(3)继续利用换元法设![]() ,设真数为
,设真数为![]() ,根据二次函数的性质可得
,根据二次函数的性质可得![]() 在
在![]() 上为增函数,则
上为增函数,则![]() ,将问题转化为方程
,将问题转化为方程![]() 在
在![]() 上有两个不同实根进行思考,再次利用换元法转化为一元二次方程,根据
上有两个不同实根进行思考,再次利用换元法转化为一元二次方程,根据![]() ,及韦达定理可计算出实数
,及韦达定理可计算出实数![]() 的取值范围.
的取值范围.
(1)![]() 时,
时,![]() ,
,
因为![]() .
.
所以![]() ,
,
所以函数![]() 的值域为
的值域为![]()
(2)设![]() ,则
,则![]() ,
,
若![]() ,则函数
,则函数![]() 无最大值,
无最大值,
即![]() 无最大值,不合题意;
无最大值,不合题意;
故![]() ,因此
,因此![]() 最大值在
最大值在![]() 时取到,
时取到,
且![]() ,所以
,所以 ,
,
解得![]() 或
或![]() ,
,
由![]() ,所以
,所以![]() .
.
(3)因为![]() 时,设
时,设![]() .设真数为
.设真数为![]() .
.
此时对称轴![]() ,
,
所以当![]() 时,
时,![]() 为增函数,且
为增函数,且![]() ,
,
即![]() 在
在![]() 上为增函数.
上为增函数.
所以,![]() ,
,
即方程![]() 在
在![]() 上有两个不同实根,
上有两个不同实根,
即![]() ,设
,设![]() .
.
所以![]() .
.
即方程![]() 有两个大于l的不等实根,
有两个大于l的不等实根,
因为![]() ,
,
所以 ,
,
解得![]() ,
,
即存在![]() ,使得函数
,使得函数![]() 为“1档类正方形函数”,且
为“1档类正方形函数”,且![]() .
.


科目:高中数学 来源: 题型:
【题目】如图设计一幅矩形宣传画,要求画面面积为4840![]() ,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面高与宽的尺寸,才能使宣传画所用纸张面积最小?
,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面高与宽的尺寸,才能使宣传画所用纸张面积最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 和平面
和平面![]() :①若直线
:①若直线![]() 与平面
与平面![]() 内的无数条直线平行,则
内的无数条直线平行,则![]() ;②若直线
;②若直线![]() 与平面
与平面![]() 内的任意一条直线都不平行,则直线
内的任意一条直线都不平行,则直线![]() 和平面
和平面![]() 相交;③若
相交;③若![]() ,则直线
,则直线![]() 与平面
与平面![]() 内某些直线平行;④若
内某些直线平行;④若![]() ,则存在平面
,则存在平面![]() 内的直线
内的直线![]() ,使
,使![]() .以上结论中正确的个数为( )
.以上结论中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的空间几何体中,平面![]() 平面
平面![]() ,
,![]() 与
与![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,BE和平面ABC所成的角为
,BE和平面ABC所成的角为![]() ,且点E在平面ABC上的射影落在
,且点E在平面ABC上的射影落在![]() 的平分线上.
的平分线上.

(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若![]() 个棱长为正整数的正方体的体积之和等于2005,求
个棱长为正整数的正方体的体积之和等于2005,求![]() 的最小值,并说明理由;
的最小值,并说明理由;
(2)若![]() 个棱长为正整数的正方体的体积之和等于
个棱长为正整数的正方体的体积之和等于![]() ,求
,求![]() 的最小值,并说明理由.
的最小值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由五个不同的数字0,1,2,5,![]() 组成无重复数字的三位数(最后结果用数字表达)
组成无重复数字的三位数(最后结果用数字表达)
(1)若![]() ,则组成的偶数有多少个?
,则组成的偶数有多少个?
(2)若![]() ,则比210大的数有多少个?
,则比210大的数有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
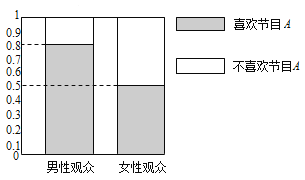
(1)根据该等高条形图,完成下列![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?

(2)从性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
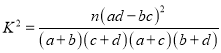 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com