练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知圆的圆心为点C（-1，2），且半径为2，求该圆在y轴上截得的线段的长度．

    分析 由题意写出圆的标准方程，取x=0得到关于y的方程，求得y，则答案可求．

    解答 解：由题意可知，圆的方程为（x+1）2+（y-2）2=4，
    取x=0，得（y-2）2=3，即y-2=$±\sqrt{3}$，
    ∴${y}_{1}=2-\sqrt{3}，{y}_{2}=2+\sqrt{3}$，
    则圆在y轴上截得的线段的长度为$|{y}_{2}-{y}_{1}|=|2+\sqrt{3}-2+\sqrt{3}|=2\sqrt{3}$．

    点评 本题考查直线与圆的位置关系，体现了方程运算思想，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届安徽六安一中高三上学期月考二数学（文）试卷（解析版） 题型：解答题

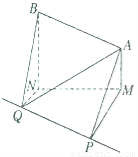
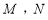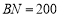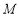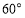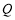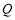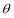    已知在东西方向上有两座小山，山顶各有一个发射塔，塔顶的海拔高度分别为米和米，一测量车在小山的正南方向的点处测得发射塔顶的仰角为，该测量车向北偏西方向行驶了米后到达点，在点处测得发射塔顶处的仰角为，恰好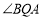的大小也等于，经测量，求两发射塔顶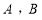之间的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

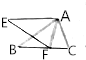    1．如图，已知△ABC≌△AEF，AB=BC，则下列结论中则下列结论正确的结论个数为（　　）
    ①AC=AF；②∠FAB=∠EAB；③EF=BC；④∠EAB=∠FAC．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=ax3+x2-ax，其中a∈R且a≠0．
    （Ⅰ）当a=1时，求函数f（x）的极值；
    （Ⅱ）求函数g（x）=$\frac{f（x）}{x}-\frac{3}{a}$lnx的单调区间；
    （Ⅲ）若存在a∈（-∞，-1]，使函数h（x）=f（x）+f′（x），x∈[-1，b]（b＞-1）在x=-1处取得最小值，试求b的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知方程x2+y2-2mx-4y+5m=0的曲线是圆C．
    （1）求m的取值范围；
    （2）当m=-2时，求圆C截直线l：2x-y+1=0所得弦长；
    （3）若圆C与直线2x-y+1=0相交于M，N两点，且以MN为直径的圆过坐标原点，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知m∈R，直线1：mx-（m2+1）y=4m和圆C：x2+y2-8x+4y+16=0相切，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．f（x）与g（x）表示同一函数的是（　　）
    A．f（x）=$\sqrt{{x}^{2}-1}$与g（x）=$\sqrt{x-1}$•$\sqrt{x+1}$B．f（x）=x与g（x）=$\frac{{x}^{3}+x}{{x}^{2}+1}$
    C．y=x与y=（$\sqrt{x}$）2D．f（x）=$\sqrt{{x}^{2}}$与g（x）=$\root{3}{{x}^{3}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆M：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点A（$\sqrt{3}，\frac{1}{2}$），离心率e=$\frac{\sqrt{3}}{2}$
    （1）求椭圆M的方程；
    （2）斜率为$\frac{\sqrt{3}}{6}$的直线l与椭圆M交于B、C两点，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知数列{an}满足a1=$\frac{71}{8}$，an+1=$\frac{7}{8}$an+1（n∈N*）
    （1）求证：数列{an-8}是等比数列，并求an；
    （2）设bn=（n+1）•（an-8），若bn≤bk对n∈N*恒成立，求正整数k的值．

    查看答案和解析>>

    同步练习册答案