
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称函数f(x)为M上的l高调函数.现给出下列命题:
①函数f(x)=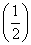 x是R上的1高调函数;
x是R上的1高调函数;
②函数f(x)=sin 2x为R上的π高调函数;
③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是[2,+∞).
其中正确的命题是________.(写出所有正确命题的序号)
科目:高中数学 来源: 题型:
下列推理中属于归纳推理且结论正确的是( )
A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2
B.由f(x)=xcos x满足f(-x)=-f(x)对∀x∈R都成立,推断:f(x)=xcos x为奇函数
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆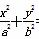 =1(a>b>0)的面积S=πab
=1(a>b>0)的面积S=πab
D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(log39)·f(log39),则a,b,c的大小关系是( )
A.b>a>c B.c>a>b
C.c>b>a D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=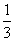 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.
(1)试问函数f(x)能否在x=-1时取得极值?说明理由;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知常数a,b,c都是实数,f(x)=ax3+bx2+cx-34的导函数为f′ (x),f′(x)≤0的解集为{x|-2≤x≤3},若f(x)的极小值等于-115,则a的值是( )
A.-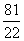 B.
B.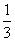
C.2 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
已知全集U={0,1,2,3,4},A={1,2,3},B={2,4},则如图阴影部分表示的集合为( )
A.{0,2} B.{0,1,3}
C.{1,3,4} D.{2,3,4}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com