
分析 根据函数奇偶性和单调性的关系将不等式进行等价转化,解不等式即可.
解答 解:∵f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增,
∴f(x)在区间(0,+∞)上单调递减,
则不等式足$f({2^{a-1}})>f(-\sqrt{2})$等价为足$f({2^{a-1}})>f(-\sqrt{2})$=f($\sqrt{2}$),
则2a-1<$\sqrt{2}$=2${\;}^{\frac{1}{2}}$,
则0<a-1<$\frac{1}{2}$,
则1<a<$\frac{3}{2}$,
故答案为:(1,$\frac{3}{2}$)
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系将不等式进行等价转化是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | c>b>a | C. | b>c>a | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
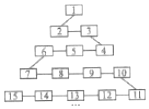 一般吧数字出现的规律满足如图的模型称为蛇形模型:数字1出现在第1行,数字2,3出现在第2行;数字6,5,4(从左到右)出现在第3行;数字7,8,9,10出现在第4行,以此类推,第21行从左到右的第4个数字应是228.
一般吧数字出现的规律满足如图的模型称为蛇形模型:数字1出现在第1行,数字2,3出现在第2行;数字6,5,4(从左到右)出现在第3行;数字7,8,9,10出现在第4行,以此类推,第21行从左到右的第4个数字应是228.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 该市在这次考试的数学平均成绩为80分 | |
| B. | 分数在120分以上的人数与分数在60分以下的人数相同 | |
| C. | 分数在110分以上的人数与分数在50分以下的人数相同 | |
| D. | 该市这次考试的数学成绩标准差为10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1<x≤0} | D. | {x|0≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{\sqrt{2}+1}{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com