
 选修4-1:几何证明选讲
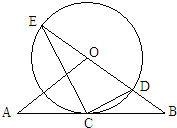
选修4-1:几何证明选讲 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
 =
= .
. =
= =
= .
.

 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
 选修4-1:几何证明选讲
选修4-1:几何证明选讲| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲
|
| 2 |
| π |
| 4 |
|
| 1-x |
| 4+2x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 选修4-1:几何证明选讲
选修4-1:几何证明选讲查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com