
分析 (1)曲线C的参数方程中用$\frac{y}{2}$代y,可得曲线C1的参数方程,化为普通方程和极坐标方程即可得到;
(2)由极坐标表示点A、A1和B、B1,运用三角形的面积公式计算△OAA1与△OBB1的面积,即可得到它们的比.
解答 解:(1)在曲线C的参数方程$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数)中用$\frac{y}{2}$代y,
得到曲线C1的参数方程$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),
化为普通方程为x2+y2=4,
故曲线C1的极坐标方程ρ=2;
(2)依题意知点A、A1的极坐标分别为(2,$\frac{π}{6}$),(2,-$\frac{π}{6}$),
设B、B1的极坐标分别为(ρ1,$\frac{π}{6}$),(ρ2,-$\frac{π}{6}$),
则ρ1ρ2=$\frac{2\sqrt{2}}{sin(\frac{π}{4}+\frac{π}{6})}$•$\frac{2\sqrt{2}}{sin(\frac{π}{4}-\frac{π}{6})}$=$\frac{8}{sin\frac{5π}{12}sin\frac{π}{12}}$=$\frac{16}{sin\frac{π}{6}}$=32,
所以${S}_{△OA{A}_{1}}$=2sin$\frac{π}{3}$=$\sqrt{3}$,
${S}_{△OB{B}_{1}}$=$\frac{1}{2}$ρ1ρ2sin$\frac{π}{3}$=16×$\frac{\sqrt{3}}{2}$=8$\sqrt{3}$,
故$\frac{{S}_{△OA{A}_{1}}}{{S}_{△OB{B}_{1}}}$=$\frac{1}{8}$.
点评 本题考查直角坐标和极坐标的转化和参数方程与极坐标方程的转化,考查运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
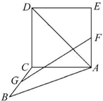 如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
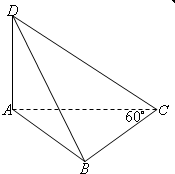 如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
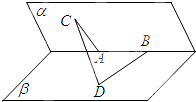 如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com