Question

下列函数中，在区间（0，1）上为增函数的是（ ）
A．
B．
C．y=sin
D．y=x²-

Answer 1

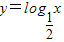
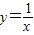
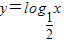【答案】分析：根据对数函数 的单调性可得应排除A，根据函数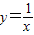在（0，1）上是减函数，故排除B，由正弦函数的单调增区间可得C满足条件，由二次函数y=x²-x 的图象和性质可得应排除D．
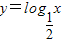解答：解：由于函数在（0，+∞）上是减函数，故函数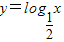在（0，1）上是减函数，故排除A．
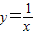由于函数在（0，+∞）上是减函数，故函数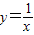在（0，1）上是减函数，故排除B．
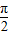由于函数y=sinx的单调增区间为[2kπ-，2kπ+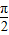]，k∈z，故在区间（0，1）上为增函数，故C满足条件．
由于二次函数y=x²-x 的图象开口向上，对称轴为x=，故函数在（0，）上是减函数，
在（，1）上是增函数，故在区间（0，1）上不是增函数，故排除D．
故选C．
点评：本题主要考查函数的单调性的判断和证明，属于基础题．