
| A. | a>0,b>0,c>0,d>0 | B. | a>0,b>0,c<0,d>0 | C. | a>0,b<0,c<0,d>0 | D. | a>0,b<0,c>0,d>0 |
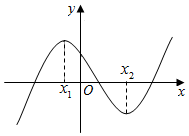
分析 根据函数的图象和性质,先判断d>0,a>0,根据二次函数的性质判断b,c的符号即可.
解答 解:f(0)=d>0,
当x→+∞时,y→+∞,
由f(x)在(-∞,x1)递增,在(x1,x2)递减,在(x2,+∞)递增,
∴函数的导数f′(x)=3ax2+2bx+c在(-∞,x1)大于0,
在(x1,x2)小于0,在(x2,+∞)大于0,
∴a>0,
函数的导数f′(x)=3ax2+2bx+c,
则f′(x)=0有两个相异的实根,
由图象得:|x2|>|x1|,
则x1+x2=-$\frac{2b}{3a}$>0且x1x2=$\frac{c}{3a}$<0,(a>0),
∴b<0,c<0,
方法2:f′(x)=3ax2+2bx+c,
由图象知当当x<x1时函数递增,当x1<x<x2时函数递减,则f′(x)对应的图象开口向上,
则a>0,且x1+x2=-$\frac{2b}{3a}$>0且x1x2=$\frac{c}{3a}$<0,(a>0),
∴b<0,c<0,
故选:C.
点评 本题主要考查函数图象的识别和判断,根据函数图象的信息,结合函数的极值及f(0)的符号是解决本题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:解答题
设 为虚数单位,
为虚数单位,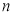 为正整数,
为正整数,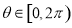 .
.
(1)用数学归纳法证明: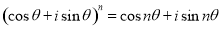 ;
;
(2)已知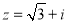 ,试利用(1)的结论计算
,试利用(1)的结论计算 ;
;
(3)设复数 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{4}{{{e^2}+5}}}$] | B. | (-∞,$\frac{4}{{{e^2}+5}}}$] | C. | [-$\frac{4}{{{e^2}+5}}$,+∞) | D. | [$\frac{4}{{{e^2}+5}}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 2或1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com