
| A. | (-∞,-$\frac{4}{{{e^2}+5}}}$] | B. | (-∞,$\frac{4}{{{e^2}+5}}}$] | C. | [-$\frac{4}{{{e^2}+5}}$,+∞) | D. | [$\frac{4}{{{e^2}+5}}$,+∞) |
分析 由求导公式和法则求出f′(x),化简后对a进行分类讨论,分别利用导数在定义域内求出函数的单调区间、最值,再求出实数a的取值范围.
解答 解:由题意得,$f′(x)=\frac{[(1-a){x}^{2}-ax+a]′{e}^{x}-({e}^{x})′[(1-a){x}^{2}-ax+a]}{({e}^{x})^{2}}$
=$\frac{(a-1){x}^{2}+(2-a)x-2a}{{e}^{x}}$=$\frac{[(a-1)x+a](x-2)}{{e}^{x}}$,
(1)当a=1时,$f′(x)=\frac{x-2}{{e}^{x}}$,
当x∈(0,2)时,f′(x)<0,f(x)在(0,2)上递减,
当x∈(2,+∞)时,f′(x)>0,f(x)在(0,2)上递增,
∴f(x)在区间[0,+∞)上有极小值f(2)=$-\frac{1}{{e}^{2}}$,
∵f(0)=a=1,且$\underset{lim}{x→∞}f(x)$=$\underset{lim}{x→∞}\frac{1-x}{{e}^{x}}$<0,
∴f(x)在区间[0,+∞)上有最大值f(0)=a=1,成立;
(2)当a>1时,由f′(x)=0得x=2或$\frac{a}{1-a}$<0,
∴当x∈(0,2)时,f′(x)<0,f(x)在(0,2)上递减,
当x∈(2,+∞)时,f′(x)>0,f(x)在(2,+∞)上递增,
∴f(x)在区间[0,+∞)上有极小值f(2)=$-\frac{1}{{e}^{2}}$,
∵f(0)=a>1,且$\underset{lim}{x→∞}f(x)$=$\underset{lim}{x→∞}\frac{(1-a){x}^{2}-a(x-1)}{{e}^{x}}$<1,
∴f(x)在区间[0,+∞)上有最大值f(0)=a,成立;
(3)当a<1时,由f′(x)=0得x=2或$\frac{a}{1-a}$,
①当a=$\frac{2}{3}$时,有2=$\frac{a}{1-a}$,f′(x)<0,则f(x)在区间[0,+∞)上递减,
∴f(x)在区间[0,+∞)上的最大值是f(0)=a,成立,
②当$\frac{2}{3}<a<1$时,有2<$\frac{a}{1-a}$,
当x∈(2,$\frac{a}{1-a}$)时,f′(x)>0,则f(x)在区间(2,$\frac{a}{1-a}$)上递增,
当x∈($\frac{a}{1-a}$,+∞)、(0,2)时,f′(x)<0,则f(x)在区间($\frac{a}{1-a}$,+∞)、(0,2)上递减,
∴f(x)在区间[0,+∞)上的极大值是f($\frac{a}{1-a}$)=$\frac{a}{{e}^{\frac{a}{1-a}}}$,
又f(0)=a,由题意得$\frac{a}{{e}^{\frac{a}{1-a}}}$≤a,解得0≤a<1,即$\frac{2}{3}<a<1$成立,
③当$a<\frac{2}{3}$时,有2>$\frac{a}{1-a}$,
当x∈($\frac{a}{1-a}$,2)时,f′(x)>0,则f(x)在区间($\frac{a}{1-a}$,2)上递增,
当x∈(2,+∞)时,f′(x)<0,则f(x)在区间(2,+∞)上递减,
∴f(x)在区间[0,+∞)上的极大值是f(2)=$\frac{4(1-a)-2a+a}{{e}^{2}}$=$\frac{4-5a}{{e}^{2}}$,
又f(0)=a,由题意得$\frac{4-5a}{{e}^{2}}$≤a,解得a≥$\frac{4}{{e}^{2}+5}$,即$a∈[\frac{4}{{e}^{2}+5},\frac{2}{3})$,
综上可得,a的取值范围是$[\frac{4}{{e}^{2}+5},+∞)$,
故选:D.
点评 本题考查了导数与函数的单调性、最值的关系,考查分类讨论思想和极限思想的应用,属于难题.


科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:填空题
设 为抛物线
为抛物线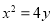 上的两动点,且线段
上的两动点,且线段 的长为6,
的长为6,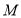 为线段
为线段 的中点,则点
的中点,则点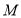 到
到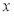 轴的最短距离为 .
轴的最短距离为 .
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
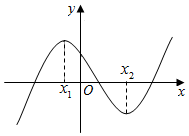
| A. | a>0,b>0,c>0,d>0 | B. | a>0,b>0,c<0,d>0 | C. | a>0,b<0,c<0,d>0 | D. | a>0,b<0,c>0,d>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com