
【题目】已知函数f(x)=x2﹣3x+alnx(a>0). (Ⅰ)若a=1,求函数f(x)的单调区间和极值;
(Ⅱ)设函数f(x)图象上任意一点的切线l的斜率为k,当k的最小值为1时,求此时切线l的方程.
【答案】解:(I)f(x)的定义域为(0,+∞), 当a=1时,f(x)=x2﹣3x+lnx,![]() .
.
由2x2﹣3x+1=0,得 ![]() ,
,
由2x2﹣3x+1>0,得 ![]() ,或x>1,∴f(x)的单调递增区间为
,或x>1,∴f(x)的单调递增区间为 ![]() ,(1,+∞).
,(1,+∞).
由2x2﹣3x+1<0,得 ![]() ,∴f(x)的单调递减区间为
,∴f(x)的单调递减区间为 ![]() .
.
∴f(x)极大值为 ![]() ;极小值为f(1)=﹣2;
;极小值为f(1)=﹣2;
(II)由题意知 ![]() ,∴a=2.
,∴a=2.
此时 ![]() ,即
,即 ![]() ,∴x=1,∴切点为(1,﹣2),
,∴x=1,∴切点为(1,﹣2),
∴此时的切线l方程为:x﹣y﹣3=0
【解析】(Ⅰ)把a=1代入原函数解析式,求导后由导函数大于0求得原函数的增区间,由导函数小于0求得原函数的减区间,从而得到极值点并求得极值;(Ⅱ)求出原函数的导函数,由基本不等式求得导函数的最小值,由导函数的最小值为1求得a的值,再由取最小值时的x值求出切点坐标,由点斜式得到切线l的方程.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,
中, ![]() :
: ![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() .
.
(1)求![]() 的普通方程及
的普通方程及![]() 的直角坐标方程,并说明它们分别表示什么曲线;
的直角坐标方程,并说明它们分别表示什么曲线;
(2)若![]() 分别为
分别为![]() ,
, ![]() 上的动点,且
上的动点,且![]() 的最小值为2,求
的最小值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市A,B两所中学的学生组队参加辩论赛,A中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.
(1)求A中学至少有1名学生入选代表队的概率;
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB.现将四边形ABCD沿EF折起,使平面ABEF⊥平面EFDC.
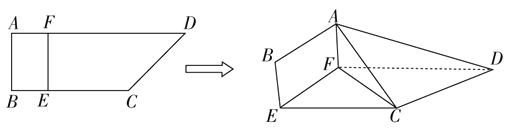
(Ⅰ)若BE=1,是否在折叠后的线段AD上存在一点P,且![]() ,使CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
,使CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
(Ⅱ)求三棱锥A-CDF的体积的最大值,并求出此时二面角E-AC-F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF![]() 平面ABCD,DE=DA=DB=2
平面ABCD,DE=DA=DB=2
(I)若G为DC的中点,求证:EG//平面BCF;
(II)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z在复平面内对应的点在第四象限,且z是方程x2﹣4x+5=0的根.
(1)求复数z;
(2)复数w=a﹣ ![]() (a∈R)满足|w﹣z|<2
(a∈R)满足|w﹣z|<2 ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +aln x(a≠0,a∈R).
+aln x(a≠0,a∈R).
(1)若a=1,求函数f(x)的极值和单调区间;
(2)若在区间(0,e]上至少存在一点x0,使得f(x0)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1
(1)求f(1)、f( ![]() )的值;
)的值;
(2)若满足f(x)+f(x﹣8)≤2,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com