
分析 如图所示,当x>1时,f(x)=lnx-1,f′(x)=$\frac{1}{x}$,令直线y=ax与曲线f(x)相切于点P(x0,lnx0-1),则a=$\frac{ln{x}_{0}-1}{{x}_{0}}$=$\frac{1}{{x}_{0}}$,解得x0=e2,可得切线斜率:$\frac{1}{{e}^{2}}$>$\frac{1}{10}$.当a=$\frac{1}{10}$时,直线y=$\frac{1}{10}$x与f(x)=$\frac{1}{10}x$+1平行,无交点,直线y=$\frac{1}{10}$x与曲线f(x)=lnx-1有两个不同交点.同理对当$0<a<\frac{1}{10}$时,当$\frac{1}{10}$≤a$<\frac{1}{{e}^{2}}$时,即可得出结论.
解答 解:如图所示,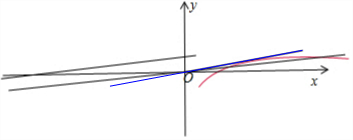
当x>1时,f(x)=lnx-1,
f′(x)=$\frac{1}{x}$,令直线y=ax与曲线f(x)相切于点P(x0,lnx0-1),则a=$\frac{ln{x}_{0}-1}{{x}_{0}}$=$\frac{1}{{x}_{0}}$,
解得x0=e2,可得切线斜率:$\frac{1}{{e}^{2}}$>$\frac{1}{10}$.
当a=$\frac{1}{10}$时,直线y=$\frac{1}{10}$x与f(x)=$\frac{1}{10}x$+1平行,无交点,直线y=$\frac{1}{10}$x与曲线f(x)=lnx-1有两个不同交点.
当$0<a<\frac{1}{10}$时,直线y=ax与曲线f(x)=lnx-1有两个不同交点,与直线y=ax有一个交点,共有3个交点,舍去.
当$\frac{1}{10}$≤a$<\frac{1}{{e}^{2}}$时,直线y=ax与曲线f(x)=lnx-1有两个不同交点,与直线y=ax没有交点.
综上可得:当$\frac{1}{10}$≤a$<\frac{1}{{e}^{2}}$时,方程f(x)=ax(a>0)恰有两个不同实数根.
故答案为:[$\frac{1}{10}$,$\frac{1}{{e}^{2}}$).
点评 本题考查了方程解的个数转化为函数图象交点的个数、利用导数研究函数的切线单调性、分类讨论方法,考查了推理能力与计算能力,属于难题.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:解答题
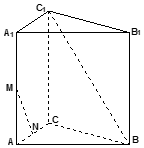 在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1,∠CAB=90°,M、N分别是AA1和AC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1,∠CAB=90°,M、N分别是AA1和AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日最高气温t(单位:℃) | t≤22℃ | 22℃<t≤28℃ | 28℃<t≤32℃ | t>32℃ |
| 天数 | 6 | 12 | X | Y |
| 高温天气 | 非高温天气 | 合计 | |
| 旺销 | 2 | 22 | 24 |
| 不旺销 | 4 | 2 | 6 |
| 合计 | 6 | 24 | 30 |
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com