
| A | 4 4 |
| A | 2 5 |
| A | 2 4 |
| A | 2 2 |
| A | 3 3 |
| A | 5 5 |
| A | 1 4 |
| A | 1 4 |
| A | 4 4 |


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
. |
| A |
. |
| A |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 9 |
A、
| ||
| B、10 | ||
| C、6 | ||
| D、9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
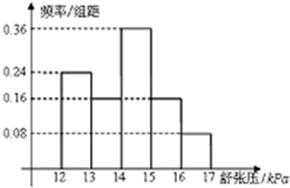 为研究某药物的疗效,选取若干志愿者进行临床研究所有志愿者舒张压数据(单位:kPa)的分组区[12,13),[13,14),[14,15﹚,[15,16﹚,[16,17﹚,将其从左到右的顺序分别编号为第一组,第二组,…第五组,如图是根据试验数据组成的频率分布直方图,已知第一组与第二组共20人,第三组中没有疗效的有6人,则第三组的人数为
为研究某药物的疗效,选取若干志愿者进行临床研究所有志愿者舒张压数据(单位:kPa)的分组区[12,13),[13,14),[14,15﹚,[15,16﹚,[16,17﹚,将其从左到右的顺序分别编号为第一组,第二组,…第五组,如图是根据试验数据组成的频率分布直方图,已知第一组与第二组共20人,第三组中没有疗效的有6人,则第三组的人数为查看答案和解析>>
科目:高中数学 来源: 题型:
| k-2x |
| 1+k•2x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com