
分析 (1)若m=1,n=2,1≤$a_1^2+a_2^2$≤1,又$a_n^2$≤1,即可求得所有满足条件的数列{an};
(2)①)当m=n=2时,1≤$a_1^2+a_2^2$≤2,由a1、a2可能取值为0,1,-1,则a1、a2取值共有:32-1=8种,
当m=n=2016时,1≤$a_1^2+a_2^2+…+a_{2016}^2$≤2016,a1、a2、a2016可能取值为0,1,-1,共有:32016-1种;
②由f(m+1,m)=3m+1-1-2m+1,将原式转换为3m+1-2m+1>2017,构造辅助函数g(m)=3m+1-2m+1,做差g(m+1)-g(m)=2×3m+1-2m+1>0,g(x)单调递增,又g(6)=2059成立,即可求得m的最小值.
解答 解:(1)当m=1,n=2时,1≤$a_1^2+a_2^2$≤1,又$a_n^2$≤1
∴{an}为0,1或0,-1或1,0或-1,0
(2)①当m=n=2时,1≤$a_1^2+a_2^2$≤2,a1、a2取值共有:32-1=8种,
即f(2,2)=8,
又当m=n=2016时,1≤$a_1^2+a_2^2+…+a_{2016}^2$≤2016,a1、a2、a2016取值共有:32016-1种;
即f(2016,2016)=32016-1f(m+1,m)>2016即1≤$a_1^2+a_2^2+…+a_{m+1}^2$≤m
②数列{an}需满足不能全为0,不能没有0(即每项均为1或-1),
∴f(m+1,m)=3m+1-1-2m+1,
即考虑3m+1-2m+1-1>2016,
令g(m)=3m+1-2m+1,
则g(m+1)-g(m)=2×3m+1-2m+1>0
∴g(m)单调增
又g(6)=2059成立,
∴m最小值为6.
点评 本题以数列为模型考查数列的取值、计数原理的应用及采用做差法求函数的单调性,考查分析问题及解决问题的能力,综合应用能力强,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
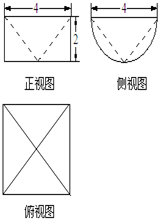
| A. | 16π-$\frac{16}{3}$ | B. | 16π-$\frac{32}{3}$ | C. | 8π-$\frac{16}{3}$ | D. | 8π-$\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com