
| 1 |
| 2 |
| . |
| A |
| 1 |
| 2 |
| C | 33 |
| 1 |
| 2 |
| C | 13 |
| 1 |
| 2 |
| • |
| ( |
| 1 |
| 2 |
| 1 |
| 8 |
| 3 |
| 8 |
| 1 |
| 2 |
| 9 |
| 6×6 |
| 1 |
| 4 |


科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| m |
| n |
| A |
| 2 |
| 3 |
| 5 |
| 1 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
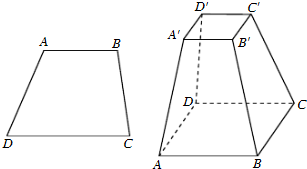 (必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.
(必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.| x |
| x+h |
| a |
| b |
| ah |
| b-a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| h |
| y-a |
| b-a |
| b-a |
| h |
| ∫ | h 0 |
| b-a |
| h |
| b-a |
| 2h |
| | | h 0 |
| b-a |
| 2h |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010年河南省郑州外国语学校高考数学模拟试卷2(理科)(解析版) 题型:解答题
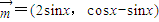 ,
,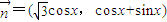 ,函数
,函数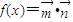 .
.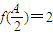 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.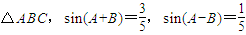 .
.查看答案和解析>>
科目:高中数学 来源:2010年河南省全真模拟(二)数学(理科)试题 题型:解答题
(本小题满分10分)请选做一题,都做时按先做的题判分,都做不加分.
(1)已知向量

①求函数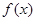 的最小正周期和值域;
的最小正周期和值域;
②在△ABC中,角A、B、C所对的边分别是a、b、c,若 且
且 ,试判断△ABC的形状.
,试判断△ABC的形状.
(2)已知锐角 .
.
①求证: ;
;
②设 ,求AB边上的高CD的长.
,求AB边上的高CD的长.
查看答案和解析>>
科目:高中数学 来源:河南省郑州外国语学校2010届高三考前全真模拟(二)(理) 题型:解答题
请选做一题,都做时按先做的题判分,都做不加分.
(1)已知向量

①求函数 的最小正周期和值域;
的最小正周期和值域;
②在△ABC中,角A、B、C所对的边分别是a、b、c,若 且
且 ,试判断△ABC的形状.
,试判断△ABC的形状.
(2)已知锐角 .
.
①求证: ;
;
②设 ,求AB边上的高CD的长.
,求AB边上的高CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com