
【题目】在△ABC中,角A、B、C所对的边分别是a、b、c,且满足csinA﹣ ![]() acosC=0.
acosC=0.
(1)求角C的大小;
(2)若c=2,求△ABC的面积S的最大值.
【答案】
(1)解:∵ ![]() ,
,
∴由正弦定理得 ![]() ,
,
∵0<A<π,
∴sinA≠0,
∴ ![]() ,
,
∵0<C<π,
∴ ![]() .
.
(2)解:由余弦定理得c2=a2+b2﹣2abcosC,又c=2, ![]() ,
,
∴4=a2+b2﹣ab,
∵a>0,b>0,
∴ab+4=a2+b2≥2ab,
∴ab≤4,当且仅当a=b=2时等号成立,
∴ ![]() ,当且仅当a=b=2时等号成立,
,当且仅当a=b=2时等号成立,
∴△ABC的面积S的最大值为 ![]() .
.
【解析】(1)由正弦定理化简已知等式可得 ![]() ,结合sinA≠0,可求
,结合sinA≠0,可求 ![]() ,结合范围0<C<π,即可求得C的值.(2)由已知及余弦定理得4=a2+b2﹣ab,结合基本不等式可求ab≤4,根据三角形的面积公式即可得解.
,结合范围0<C<π,即可求得C的值.(2)由已知及余弦定理得4=a2+b2﹣ab,结合基本不等式可求ab≤4,根据三角形的面积公式即可得解.
【考点精析】关于本题考查的正弦定理的定义,需要了解正弦定理:![]() 才能得出正确答案.
才能得出正确答案.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
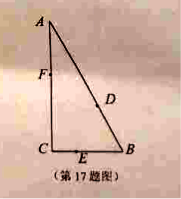
【题目】【2017镇江一模】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,
,
斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,所在位
大道上嬉戏,所在位
置分别记为点![]() .
.
(1)若甲乙都以每分钟![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,到大道的另一端
出发在各自的大道上奔走,到大道的另一端
时即停,乙比甲迟![]() 分钟出发,当乙出发
分钟出发,当乙出发![]() 分钟后,求此时甲乙两人之间的距离;
分钟后,求此时甲乙两人之间的距离;
(2)设![]() ,乙丙之间的距离是甲乙之间距离的
,乙丙之间的距离是甲乙之间距离的![]() 倍,且
倍,且![]() ,请将甲
,请将甲
乙之间的距离![]() 表示为
表示为![]() 的函数,并求甲乙之间的最小距离.
的函数,并求甲乙之间的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】100辆汽车通过某一段公路时,时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约有( )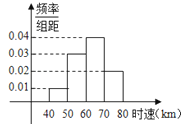
A.60辆
B.80辆
C.70辆
D.140辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017福建三明5月质检】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
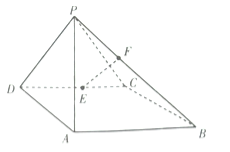
(Ⅰ)求证: ![]() ;
;
(Ⅱ)试确定点![]() 的位置,使得直线
的位置,使得直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面坐标系内,O为坐标原点,向量 ![]() =(1,7),
=(1,7), ![]() =(5,1),
=(5,1), ![]() =(2,1),点M为直线OP上的一个动点.
=(2,1),点M为直线OP上的一个动点.
(1)当 ![]()
![]() 取最小值时,求向量
取最小值时,求向量 ![]() 的坐标;
的坐标;
(2)在点M满足(I)的条件下,求∠AMB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,过椭圆M: ![]() (a>b>0)右焦点的直线x+y﹣
(a>b>0)右焦点的直线x+y﹣ ![]() =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为 ![]() .
.
(Ⅰ)求M的方程
(Ⅱ)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是
),则下面结论正确的是
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com