
【题目】已知对称轴为坐标轴的双曲线有一条渐近线为2x﹣y=0,则该双曲线的离心率为 .
【答案】![]() 或
或![]()
【解析】
试题当双曲线焦点在x轴上时,可设标准方程为![]() (a>0,b>0),此时渐近线方程是
(a>0,b>0),此时渐近线方程是![]() ,与已知条件中的渐近线方程比较可得b=2a,最后用平方关系可得c=
,与已知条件中的渐近线方程比较可得b=2a,最后用平方关系可得c=![]() a,用公式可得离心率e=
a,用公式可得离心率e=![]() =
=![]() ;当双曲线焦点在y轴上时,用类似的方法可得双曲线的离心率为
;当双曲线焦点在y轴上时,用类似的方法可得双曲线的离心率为![]() .由此可得正确答案.
.由此可得正确答案.
解:(1)当双曲线焦点在x轴上时,
设它的标准方程为![]() (a>0,b>0)
(a>0,b>0)
∵双曲线的一条渐近线方程是2x﹣y=0,
∴双曲线渐近线方程是![]() ,即y=±2x
,即y=±2x
∴![]() b=2a
b=2a
∵c2=a2+b2
∴![]() =
=![]() =
=![]() a
a
所以双曲线的离心率为e=![]() =
=![]()
(2)当双曲线焦点在y轴上时,
设它的标准方程为![]() (a>0,b>0)
(a>0,b>0)
采用类似(1)的方法,可得![]()
![]()
∴![]() =
=![]() =
=![]()
所以双曲线的离心率为e=![]() =
=![]()
综上所述,该双曲线的离心率为![]() 或
或![]()
故答案为![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于![]() 四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
(1)求恰有1人申请![]() 片区房源的概率;
片区房源的概率;
(2)用![]() 表示选择
表示选择![]() 片区的人数,求
片区的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拟用10万元投资甲、乙两种商品.已知各投入![]() 万元,甲、乙两种商品分别可获得
万元,甲、乙两种商品分别可获得![]() 万元的利润,利润曲线
万元的利润,利润曲线![]() ,
,![]() ,如图所示.
,如图所示.
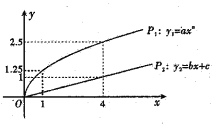
(1)求函数![]() 的解析式;
的解析式;
(2)应怎样分配投资资金,才能使投资获得的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
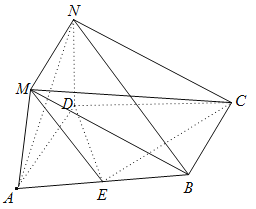
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.![]() ,
,![]() ,
,![]() 且点
且点![]() 为
为![]() 的中点.
的中点.
(1) 求证:![]()
![]() 平面
平面![]() ;
;
(2) 求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据教育部高考改革指导意见,广东省从2021年正式实施“![]() ”新的高考考试方案.为尽快了解学生的选科需求,及时调整学校人力资源配备.某校从高一学生中抽样调查了100名同学,在模拟分科选择中,一半同学(其中男生38人)选择了物理,另一半(其中男生14人)选择了历史.请完成以下
”新的高考考试方案.为尽快了解学生的选科需求,及时调整学校人力资源配备.某校从高一学生中抽样调查了100名同学,在模拟分科选择中,一半同学(其中男生38人)选择了物理,另一半(其中男生14人)选择了历史.请完成以下![]() 列联表,并判断能否有99.9%的把握说选科与性别有关?
列联表,并判断能否有99.9%的把握说选科与性别有关?
参考公式: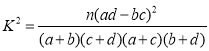 ,其中
,其中![]() 为样本容量.
为样本容量.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | |||
选物理 | 选历史 | 总计 | ||||||||
男生 | ||||||||||
女生 | ||||||||||
总计 | ||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4-4:坐标系与参数方程)
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是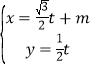 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com