
【题目】(选修4-4:坐标系与参数方程)
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是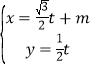 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A. ![]() =(0,0),
=(0,0),![]() =(1,2)B.
=(1,2)B. ![]() =(-1,2),
=(-1,2),![]() =(5,-2)
=(5,-2)
C. ![]() =(3,5),
=(3,5),![]() =(6,10)D.
=(6,10)D. ![]() =(2,-3),
=(2,-3),![]() =(-2,3)
=(-2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)![]() 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求![]() 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数![]() 满足
满足![]() ,则称
,则称![]() 为这三个数的中位数).
为这三个数的中位数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() 为参数),A,B是C上的动点,且满足
为参数),A,B是C上的动点,且满足![]() (O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为
(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为![]() .
.
(1)求椭圆C的极坐标方程和点D的直角坐标;
(2)利用椭圆C的极坐标方程证明 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知PC⊥BC,PC⊥AC,点E,F,G分别是所在棱的中点,则下面结论中错误的是 ( )

A.平面EFG∥平面PBC
B.平面EFG⊥平面ABC
C.∠BPC是直线EF与直线PC所成的角
D.∠FEG是平面PAB与平面ABC所成二面角的平面角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区工会利用“健步行![]() ”开展明年健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为
”开展明年健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九组,整理得到如下频率分布直方图:
九组,整理得到如下频率分布直方图:
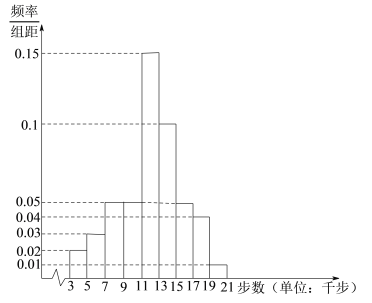
(1)从当天步数在![]() ,
,![]() ,
,![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于220分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于220分的概率;
(2)求该组数据的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
(1)求下表中z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数![]() 记这8辆轿车的得分的平均数为
记这8辆轿车的得分的平均数为![]() ,定义事件
,定义事件![]() {
{![]() ,且函数
,且函数![]() 没有零点},求事件
没有零点},求事件![]() 发生的概率
发生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计学中,经常用环比、同比来进行数据比较,环比是指本期统计数据与上期比较,如![]() 年
年![]() 月与
月与![]() 年
年![]() 月相比,同比是指本期数据与历史同时期比较,如
月相比,同比是指本期数据与历史同时期比较,如![]() 年
年![]() 月与
月与![]() 年
年![]() 月相比.
月相比.
环比增长率![]() (本期数
(本期数![]() 上期数)
上期数)![]() 上期数
上期数![]() ,
,
同比增长率![]() (本期数
(本期数![]() 同期数)
同期数)![]() 同期数
同期数![]() .
.
下表是某地区近![]() 个月来的消费者信心指数的统计数据:
个月来的消费者信心指数的统计数据:
序号 |
|
|
|
|
|
|
|
|
时间 |
|
|
|
|
|
|
|
|
消费者信心指数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017年
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() 求该地区
求该地区![]() 年
年![]() 月消费者信心指数的同比增长率(百分比形式下保留整数);
月消费者信心指数的同比增长率(百分比形式下保留整数);
![]() 除
除![]() 年
年![]() 月以外,该地区消费者信心指数月环比增长率为负数的有几个月?
月以外,该地区消费者信心指数月环比增长率为负数的有几个月?
![]() 由以上数据可判断,序号
由以上数据可判断,序号![]() 与该地区消费者信心指数
与该地区消费者信心指数![]() 具有线性相关关系,写出
具有线性相关关系,写出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 保留
保留![]() 位小数),并依此预测该地区
位小数),并依此预测该地区![]() 年
年![]() 月的消费者信心指数(结果保留
月的消费者信心指数(结果保留![]() 位小数,参考数据与公式:
位小数,参考数据与公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
, )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com