
用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
科目:高中数学 来源: 题型:
一个袋中有大小、质地相同的标号为 的三个小球.某人做如下游戏:每次从袋中摸一个小球,记下标号然后放回,共摸球
的三个小球.某人做如下游戏:每次从袋中摸一个小球,记下标号然后放回,共摸球 次.若拿出球的标号是奇数,则得
次.若拿出球的标号是奇数,则得 分,否则得
分,否则得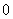 分,则
分,则 次所得分数之和的数学期望是 .
次所得分数之和的数学期望是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
命题:“若空间两条直线a,b分别垂直于平面α,则a∥b.”学生小夏这样证明:设a,b与面α分别相交于A,B,连接A,B.
∵a⊥α,b⊥α,AB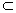 α,①
α,①
∴a⊥AB,b⊥AB,②
∴a∥b.③
这里的证明有两个推理,p:①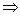 ②,q:②
②,q:②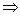 ③,则下列命题为真命题的是( ).
③,则下列命题为真命题的是( ).
A.p∧q B.p∨q
C.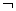 p∨q D.(
p∨q D.(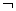 p)∧(
p)∧(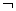 q)
q)
查看答案和解析>>
科目:高中数学 来源: 题型:
如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
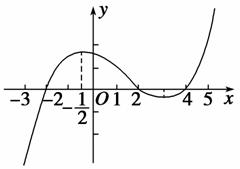 ①函数y=f(x)在区间
①函数y=f(x)在区间 内单调递增;
内单调递增;
②函数y=f(x)在区间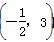 内单调递减;
内单调递减;
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x=-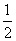 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断正确的是________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照 ,
,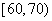 ,
, ,
, ,
,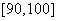 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
,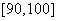 的数据).
的数据).

(1)求样本容量n和频率分布直方图中x,y的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设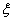 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在 的学生个数,求
的学生个数,求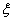 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com