
 已知:如图,在单位正方体ABCD-A1B1C1D1中,M是A1B上的点,A1M=
已知:如图,在单位正方体ABCD-A1B1C1D1中,M是A1B上的点,A1M=| 1 |
| 3 |
| 1 |
| 3 |
| MN |
| A1B |
| MN |
| B1D1 |
| MN |
 (1)证明:建立如图所示空间直角坐标系,设正方体的棱长为1,
(1)证明:建立如图所示空间直角坐标系,设正方体的棱长为1,| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| A1B |
| B1D1 |
| MN |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| MN |
| A1B |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| MN |
| B1D1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| MN |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(
|
| ||
| 3 |
| ||
| 3 |


科目:高中数学 来源: 题型:
 选修4-2:矩阵及其变换
选修4-2:矩阵及其变换| OA |
| OB |
| OA′ |
| OB′ |
| π |
| 3 |
|
| 5 |
| 5 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
查看答案和解析>>
科目:高中数学 来源: 题型:
 请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.
请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.| BF |
| FC |
| π |
| 6 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 10 |
2
| ||
| 5 |
| 19π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省四地六校联考高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
 被矩阵M作用后分别变成
被矩阵M作用后分别变成 ,
, 在M作用后的函数解析式;
在M作用后的函数解析式; (t为参数),在极坐标系(与直角坐标系x0y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系x0y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
. ),求|PA|+|PB|.
),求|PA|+|PB|. ,求x+4y+9z的最小值及取得最小值时x,y,z的值.
,求x+4y+9z的最小值及取得最小值时x,y,z的值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省四地六校联考高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
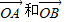 被矩阵M作用后分别变成
被矩阵M作用后分别变成 ,
, 在M作用后的函数解析式;
在M作用后的函数解析式; (t为参数),在极坐标系(与直角坐标系x0y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系x0y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
. ),求|PA|+|PB|.
),求|PA|+|PB|. ,求x+4y+9z的最小值及取得最小值时x,y,z的值.
,求x+4y+9z的最小值及取得最小值时x,y,z的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com