
【题目】随着人们对环境关注度的提高,绿色低碳出行越来越受到市民重视. 为此贵阳市建立了公共自行车服务系统,市民凭本人二代身份证到自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20积分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.3.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【答案】(1)甲、乙两人所扣积分相同的概率为0.36,(2)![]() 的数学期望
的数学期望![]() .
.
【解析】试题分析:(1)先确定甲、乙两人所扣积分相同事件取法:扣0分、扣1分及扣2分,再根据相互独立事件概率乘法公式及互斥事件概率加法公式得所求概率,(2)先确定随机变量取法,再分别求对应概率,列表可得分布列,最后根据数学期望公式求期望.
试题解析:(Ⅰ)分别记“甲扣0,1,2分”为事件![]() ,它们彼此互斥,
,它们彼此互斥,
且![]() .
.
分别记“乙扣0,1,2分”为事件![]() ,它们彼此互斥,
,它们彼此互斥,
且![]() .
.
由题知, ![]() 与
与![]() 相互独立,
相互独立,
记甲、乙两人所扣积分相同为事件![]() ,则
,则![]() ,
,
所以![]()
=![]() .
.
(Ⅱ)![]() 的可能取值为:
的可能取值为: ![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | 4 |
P | 0.2 | 0.32 | 0.3 | 0.14 | 0.04 |
![]() 的数学期望
的数学期望![]() .
.
答:甲、乙两人所扣积分相同的概率为0.36, ![]() 的数学期望
的数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最低点为
,且图象上一个最低点为 ![]() .
.
(1)求f(x)的解析式;
(2)当 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥S﹣ABC中,SA⊥AB,SA⊥AC,AC⊥BC且AC=2,BC=![]() , SB=
, SB=![]() .
.
(1)证明:SC⊥BC;
(2)求三棱锥的体积VS﹣ABC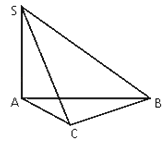
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t≤1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).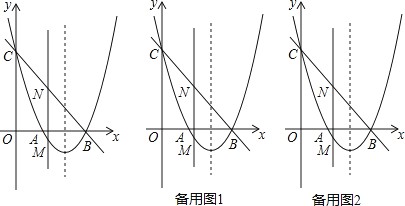
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为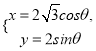 (
(![]() 为参数),设直线
为参数),设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求线段![]() 的长;
的长;
(Ⅱ)已知点![]() 在曲线
在曲线![]() 上运动,当
上运动,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标及
的坐标及![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D上方时,写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com