
(本小题共13分)已知函数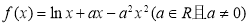 .
.
(Ⅰ)若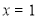 是函数
是函数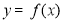 的极值点,求
的极值点,求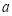 的值;
的值;
(Ⅱ)求函数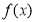 的单调区间.
的单调区间.
(Ⅰ) 或
或 .(Ⅱ)当
.(Ⅱ)当 时,单调递增区间是
时,单调递增区间是 ,单调递减区间是
,单调递减区间是 ,当
,当 时,单调递增区间是
时,单调递增区间是 ,单调递减区间是
,单调递减区间是 .
.
【解析】
试题分析:(Ⅰ)由极值点概念得 ,可解出
,可解出 或
或 .但这是必要条件,需验证其充分性,即列表分析导数值在
.但这是必要条件,需验证其充分性,即列表分析导数值在 附近是否变号(Ⅱ)首先求得:
附近是否变号(Ⅱ)首先求得: ,再利用导数的符号判断函数
,再利用导数的符号判断函数 的单调性并求单调区间;在确定导数的符号时需根据导函数零点有无及大小进行分类讨论:当
的单调性并求单调区间;在确定导数的符号时需根据导函数零点有无及大小进行分类讨论:当 时,
时, 为导函数一个零点;当
为导函数一个零点;当 时,
时, 为导函数一个零点;再列表分析即得
为导函数一个零点;再列表分析即得
试题解析:(Ⅰ)函数 的定义域为
的定义域为 . 1分
. 1分

 . 3分
. 3分
因为 是函数
是函数 的极值点,所以
的极值点,所以 . 5分
. 5分
解得 或
或 .
.
经检验, 或
或 时,
时, 是函数
是函数 的极值点. 6分
的极值点. 6分
(Ⅱ)由(Ⅰ)知:
 .
.
由 ,令
,令 ,解得
,解得 . 9分
. 9分
当 时,
时,  的变化情况如下表
的变化情况如下表
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
∴函数 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 ; 11分
; 11分
当 时,
时, 的变化情况如下表
的变化情况如下表
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
∴函数 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 . 13分
. 13分
考点:极值点,利用导数求单调区间


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:
如图所示,直三棱柱ABC-A1B1C1,在底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
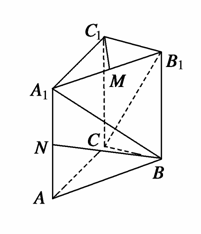
(1)求BN的长;
(2)求异面直线BA1与CB1所成角的余弦值;
(3)求证:A1B⊥C1M.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市石景山区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
A , B两地街道如图所示,某人要从A地前往B地,则路程最短的走法有 种(用数字作答).

查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市石景山区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
如果实数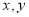 满足不等式组
满足不等式组 目标函数
目标函数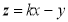 的最大值为6,最小值为0,则实数
的最大值为6,最小值为0,则实数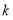 的值为( )
的值为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市丰台区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
在复平面内,复数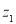 ,
,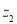 对应的点分别是A,B(如图所示),则复数
对应的点分别是A,B(如图所示),则复数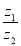 的值是 .
的值是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高三三月阶段测试文科数学试卷(解析版) 题型:解答题
(本题满分15分)已知各项均为正数的数列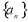 的前
的前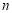 项和为
项和为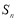 ,且
,且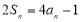 . 在数列
. 在数列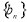 中,
中,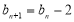 ,
,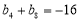 .
.
(Ⅰ)求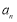 ,
,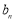 ;
;
(Ⅱ)设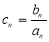 求数列
求数列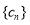 的前项和
的前项和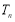 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com