练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，直三棱柱ABC－A1B1C1，在底面△ABC中，CA＝CB＝1，∠BCA＝90°，棱AA1＝2，M、N分别是A1B1、A1A的中点．

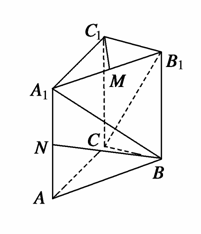
    (1)求BN的长；

    (2)求异面直线BA1与CB1所成角的余弦值；

    (3)求证：A1B⊥C1M.


    [解析]　

    如图所示，以C为原点建立空间直角坐标系C—xyz.

    (1)依题意得B(0,1,0)，N(1,0,1)．

    ∴BN的长为.

    (2)依题意得A1(1,0,2)，B(0,1,0)，C(0,0,0)，B1(0,1,2)，

    ∴异面直线BA1与CB1所成角的余弦值为.

    (3)依题意得C1(0,0,2)，M(，，2)，

    ＝(－1,1，－2)，＝(，，0)．

    ∴·＝－＋＋0＝0.

    ∴⊥∴A1B⊥C1M.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


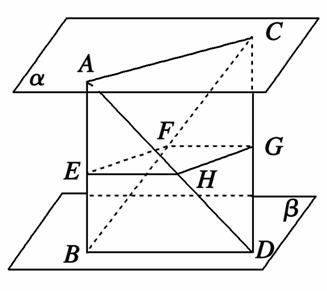
    如图，已知α∥β，异面直线AB，CD和平面α，β分别交于A，B，C，D四点，E，F，G，H分别是AB，BC，CD，DA的中点．

    求证：(1)E，F，G，H共面；

    (2)平面EFGH∥平面α.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    A(－3,1,5)，B(4,3,1)的中点坐标是(　　)

    A．(，1，－2)                                          B．(，2,3)

    C．(－12,3,5)                                                D．(，3,2)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知A(－1,0,1)、B(x，y,4)、C(1,4,7)，且A、B、C三点在同一条直线上，则实数x、y分别等于(　　)

    A．x＝0，y＝1                                              B．x＝0，y＝2

    C．x＝1，y＝1                                              D．x＝1，y＝2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在下列命题中：

    ①若向量a，b共线，则向量a，b所在的直线平行；

    ②若向量a，b所在的直线为异面直线，则向量a，b一定不共面；

    ③若三个向量a，b，c两两共面，则向量a，b，c共面；

    ④已知空间的三个向量a，b，c，则对于空间的任意一个向量p总存在实数x，y，z使得p＝xa＋yb＋zc.

    其中正确命题的个数是(　　)

    A．0                                                             B．1

    C．2                                                             D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正方体ABCD－A1B1C1D1中BB1与平面ACD1所成角的余弦值为(　　)

    A.                                                          B.

    C.                                                             D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如下图，正方形ABCD与矩形ACEF所在平面互相垂直，AB＝，AF＝1.M在EF上，且AM∥平面BDE.则M点的坐标为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设直线l的方程为x＋ycosθ＋3＝0(θ∈R)，则直线l的倾斜角α的范围是(　　)

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年北京市石景山区高三上学期期末考试理科数学试卷（解析版） 题型：解答题

    （本小题共13分）已知函数.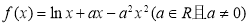

    （Ⅰ）若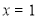是函数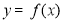的极值点，求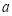的值；

    （Ⅱ）求函数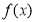的单调区间.

    查看答案和解析>>

    同步练习册答案