【题目】已知函数f(x)的定义域为{x|x∈R，且x≠0}，对定义域内的任意x1、x2，都有f(x1·x2)＝f(x1)＋f(x2)，且当x>1时，f(x)>0.
(1)求证：f(x)是偶函数；
(2)求证：f(x)在(0，＋∞)上是增函数．
【答案】（1）见解析 （2）见解析
【解析】证明： (1)因对定义域内的任意x1、x2都有
f(x1·x2)＝f(x1)＋f(x2)，
令x1＝x，x2＝－1，
则有f(－x)＝f(x)＋f(－1)．
又令x1＝x2＝－1，得2f(－1)＝f(1)．
再令x1＝x2＝1，得f(1)＝0，
从而f(－1)＝0，
于是有f(－x)＝f(x)，所以f(x)是偶函数．
(2)设0<x1<x2，
则f(x1)－f(x2)＝f(x1)－f(x1·
)＝f(x1)－[f(x1)＋f(
)]＝－f(
)，
由于0<x1<x2，所以
>1，从而f(
)>0，
故f(x1)－f(x2)<0，即f(x1)<f(x2)，
所以f(x)在(0，＋∞)上是增函数．
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案科目：高中数学 来源： 题型：
【题目】数列{an}满足a1= 
，an+1﹣1=an（an﹣1）（n∈N*）且Sn= 
+ 
+…+ 
，则Sn的整数部分的所有可能值构成的集合是（ ）
A.{0，1，2}
B.{0，1，2，3}
C.{1，2}
D.{0，2}
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合A=[0， 
），B=[ ，1]，函数f （x）=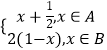 
，若x0∈A，且f[f （x0）]∈A，则x0的取值范围是（ ）
A.（0， 
]
B.[ ， ]
C.（ ， ）
D.[0， 
]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）是定义在（﹣∞，+∞）上的偶函数，且它在[0，+∞）上单调递增，若a=f（ 
），b=f（ 
），c=f（﹣2），则a，b，c的大小关系是（从小到大排）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知AB是⊙O的直径，点D是⊙O上一点，过点D作⊙O的切线，交AB的延长线于点C，过点C作AC的垂线，交AD的延长线于点E．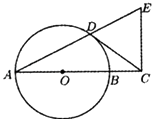 
（1）求证：△CDE为等腰三角形；
（2）若AD=2， 
= 
，求⊙O的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给定椭圆
，称圆
为椭圆
的“伴随圆”.已知点
是椭圆
上的点
（1）若过点
的直线
与椭圆
有且只有一个公共点，求
被椭圆
的伴随圆
所截得的弦长：
（2）
是椭圆
上的两点，设
是直线
的斜率，且满足
，试问：直线
是否过定点，如果过定点，求出定点坐标，如果不过定点，试说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
