Question

【题目】如图1，2，在Rt△ABC中，AB=BC=4，点E在线段AB上，过点E作交AC于点F，将△AEF沿EF折起到△PEF的位置（点A与P重合），使得∠PEB=60°．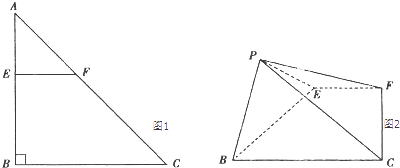

（1）求证：EF⊥PB；
（2）试问：当点E在何处时，四棱锥P﹣EFCB的侧面的面积最大？并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值．

Answer 1

【答案】
（1）证明：∵EF∥BC且BC⊥AB，

∴EF⊥AB，即EF⊥BE，EF⊥PE．又BE∩PE=E，

∴EF⊥平面PBE，又PB平面PBE，

∴EF⊥PB

（2）解：设BE=x，PE=y，则x+y=4．

∴ ．

当且仅当x=y=2时，S△PEB的面积最大，此时，BE=PE=2．

由（1）知EF⊥平面PBE，

∵EF平面EFCB，∴平面EFCB⊥平面PBE．

在平面PBE中，作PO⊥BE于O，则PO⊥平面EFCB．

即PO为四棱锥P﹣EFCB的高．

又 ．

∴

∵ ，

∴BO=1，在Rt△OBC中， ．

∵PO⊥平面EFCB，∴∠PCO就是PC与平面EFCB所成角．

∴ ，

故直线PC与平面EFCB所成角的正切值为

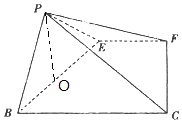
【解析】（1）推导出EF⊥AB，EF⊥BE，EF⊥PE，由此能证明EF⊥PB．　（2）设BE=x，PE=y，则x+y=4，当且仅当x=y=2时，S△PEB的面积最大，此时，BE=PE=2．EF⊥平面PBE，从而平面EFCB⊥平面PBE．作PO⊥BE于O，则PO为四棱锥P﹣EFCB的高，∠PCO就是PC与平面EFCB所成角．由此能求出结果．