
已知函数f(x)=lnx-mx(m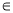 R).
R).
(1)若曲线y=f(x)过点P(1,-1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1,x2,求证:x1x2>e2.
(1)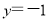 ;(2)①当
;(2)①当 时,
时, ;②当
;②当 时,
时,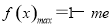
③当 时,
时,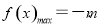 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)根据题意首先由点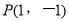 在曲线
在曲线 上,运用待定系数的方法求出
上,运用待定系数的方法求出 ,再由切线与导数的关系即可求出切线方程为
,再由切线与导数的关系即可求出切线方程为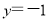 ;(2)对函数求导可得:
;(2)对函数求导可得: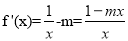 ,分析m对导数的影响,可见要进行分类讨论:①当
,分析m对导数的影响,可见要进行分类讨论:①当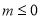 时,
时,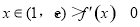 ,所以函数
,所以函数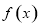 在
在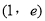 上单调递增,利用单调性可求出最大值;②当
上单调递增,利用单调性可求出最大值;②当 ,即
,即 时,
时,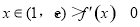 ,所以函数
,所以函数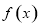 在
在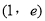 上单调递增,利用单调性可求出最大值;③当
上单调递增,利用单调性可求出最大值;③当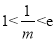 ,即
,即 时,导数有下有负,列表可求出函数的最大值;④当
时,导数有下有负,列表可求出函数的最大值;④当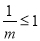 ,即
,即 时,
时,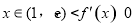 ,所以函数
,所以函数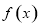 在
在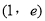 上单调递减,利用单调性可求出最大值;(3)显然两零点均为正数,故不妨设
上单调递减,利用单调性可求出最大值;(3)显然两零点均为正数,故不妨设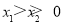 ,由零点的定义可得:
,由零点的定义可得: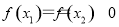 ,即
,即 ,观察此两式的结构特征可相加也可相减化简得:
,观察此两式的结构特征可相加也可相减化简得: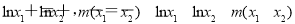 ,现在我们要证明
,现在我们要证明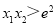 ,即证明
,即证明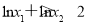 ,也就是
,也就是 .又因为
.又因为 ,所以即证明
,所以即证明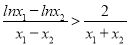 ,即
,即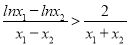 .由它的结构可令
.由它的结构可令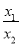 =t,则
=t,则 ,于是
,于是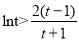 .构造一新函数
.构造一新函数 ,将问题转化为求此函数的最小值大于零,即可得证.
,将问题转化为求此函数的最小值大于零,即可得证.
试题解析:(1)因为点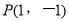 在曲线
在曲线 上,所以
上,所以 ,解得
,解得 .
.
因为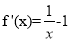 ,所以切线的斜率为0,所以切线方程为
,所以切线的斜率为0,所以切线方程为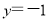 . 3分
. 3分
(2)因为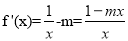 .
.
①当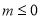 时,
时,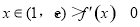 ,所以函数
,所以函数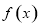 在
在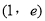 上单调递增,则
上单调递增,则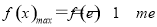 .
.
②当 ,即
,即 时,
时,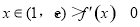 ,所以函数
,所以函数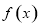 在
在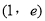 上单调递增,则
上单调递增,则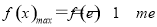 5分
5分
③当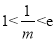 ,即
,即 时,函数
时,函数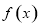 在
在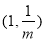 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
则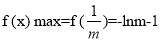 . 7分
. 7分
④当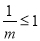 ,即
,即 时,
时,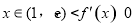 ,所以函数
,所以函数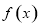 在
在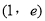 上单调递减,则
上单调递减,则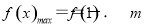 9分
9分
综上,①当 时,
时, ;
;
②当 时,
时,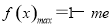
③当 时,
时,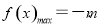 . 10分
. 10分
(3)不妨设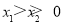 .因为
.因为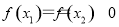 ,所以
,所以 ,
,
可得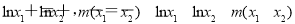 .
.
要证明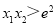 ,即证明
,即证明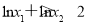 ,也就是
,也就是 .
.
因为 ,所以即证明
,所以即证明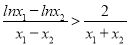 ,即
,即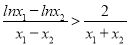 . 12分
. 12分
令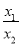 =t,则
=t,则 ,于是
,于是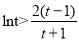 .
.
令 ,则
,则 .
.
故函数 在
在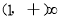 上是增函数,所以
上是增函数,所以 ,即
,即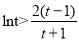 成立.
成立.
所以原不等式成立. 16分
考点:1.曲线的切线;2.函数与导数的综合运用;3.函数的零点与方程的根


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:解答题
为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中
释放的浓度y(单位:毫克/立方米)随着时间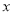 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为

若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之
和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a( )个单位的药剂,要使接下来的4天中能够持续有效净化,试求
)个单位的药剂,要使接下来的4天中能够持续有效净化,试求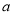 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: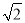 取1.4).
取1.4).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
设二次函数f(x)=ax2+bx+c(a,b,c为常数)的导函数为f′(x).对任意x∈R,不等式f(x)≥f′(x)恒成立,则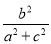 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟理科数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,P为不等式组 所表示的平面区域内一动点,则线段|OP|的最小值等于 .
所表示的平面区域内一动点,则线段|OP|的最小值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com