科目：高中数学 来源：2016届山西省榆林市高三二模理科数学试卷（解析版） 题型：解答题
选修4-4：坐标系与参数方程
已知极坐标的极点与直角坐标系的原点重合，极轴与
正半轴重合，且长度单位相同，直线的极坐标方程为
，点
，（参数
）.
（1）求点
轨迹的直角坐标方程；
（2）求点
到直线
距离的最大值.
查看答案和解析>>
科目：高中数学 来源：2016届吉林省高三五模理科数学试卷（解析版） 题型：选择题
公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，正多边形的周长可无限逼近于圆的周长，并创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14 ，这就是著名的徽率，利用刘徽的割圆术设计的程序框图，如图所示，则输出的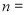
（ ）
（参考数据：
）
A．48 B．96 C．192 D．384
查看答案和解析>>
科目：高中数学 来源：2015-2016学年贵州遵义一中高二下联考理科数学试卷（解析版） 题型：解答题
在一次考试中，5名同学的数学、物理成绩如下表所示：
学生 |
|
|
|
|
|
数学（ | 89 | 91 | 93 | 95 | 97 |
物理（ | 87 | 89 | 89 | 92 | 93 |
（1）根据表中数据，求物理分
对数学分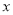
的回归直线方程；
（2）要从4名数学成绩在90分以上的同学中选出2名参加一项活动，以
表示选中的同学中物理成绩高于90分的人数，求随机变最
的分布列及数学期望
.
附：回归方程
，
，
，其中
为样本平均数.
查看答案和解析>>
科目：高中数学 来源：2015-2016学年贵州遵义一中高二下联考理科数学试卷（解析版） 题型：选择题
已知中心在原点的椭圆与双曲线有公共焦点，左，右焦点分别为
，且两条曲线在第一象限的交点为
，
是以
为底边的等腰三角形，若
，椭圆与双曲线的离心率分别为
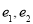，则
的取值范围是（ ）
A．
B．
C．
D．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
,若
,则实数
的取值范围是（ ）
B．
C．
D．
满足约束条件
，且点
，则
的取值范围是（ ）
B．
C．
D．
满足
，则
的取值范围是 ．
满足
，则
的共轭复数的虚部是（ ）
B．
C．
D．