
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,正多边形的周长可无限逼近于圆的周长,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14 ,这就是著名的徽率,利用刘徽的割圆术设计的程序框图,如图所示,则输出的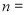 ( )
( )
(参考数据: )
)

A.48 B.96 C.192 D.384
科目:高中数学 来源:2015-2016学年贵州遵义一中高一下第二次联考数学试卷(解析版) 题型:选择题
已知等差数列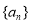 中,前
中,前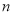 项和
项和 ,若
,若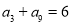 ,则
,则 ( )
( )
A.12 B.33 C.66 D.99
查看答案和解析>>
科目:高中数学 来源:2016届吉林省高三五模文科数学试卷(解析版) 题型:选择题
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,正多边形的面积可无限逼近于圆的面积,并创立了割圆术,即所谓“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”。利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14 ,这就是著名的徽率,利用刘徽的割圆术设计的程序框图,如图所示,则输出的 ( )
( )
(参考数据: )
)

A.24 B.48 C.96 D.192
查看答案和解析>>
科目:高中数学 来源:2016届吉林省高三五模理科数学试卷(解析版) 题型:解答题
为配合4月23日“世界读书日”,某校将4月18日-4月24日定为学校读书周,并从全校学生中随机抽取 名学生,获得了他们一周课外读书时间(单位:小时)的数据如下:
名学生,获得了他们一周课外读书时间(单位:小时)的数据如下:

(1)求 的值及该校读书周人均读书时间估计值;
的值及该校读书周人均读书时间估计值;
(2)如果按读书时间 用分层抽样的方法从
用分层抽样的方法从 名学生中抽取20人,再从这20人中随机选取3人,记
名学生中抽取20人,再从这20人中随机选取3人,记 为课外读书时间落在
为课外读书时间落在 的人数,求
的人数,求 的分布列和数学期望;
的分布列和数学期望;
(3)将样本频率视为概率,从该校学生中随机选取3人,记 表示课外读书时间落在
表示课外读书时间落在 的人数,求
的人数,求 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高三最后一卷文科数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程
的参数方程 (
( 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com