
【题目】椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的两个动点,若直线
上的两个动点,若直线![]() 的斜率乘积为定值
的斜率乘积为定值![]() ,则动直线
,则动直线![]() 恒过定点的坐标为__________.
恒过定点的坐标为__________.
【答案】![]()
【解析】当直线BC的斜率存在时,设直线BC的方程为y=kx+m,
由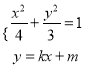 ,消去y得:(3+4k2)x2+8kmx+4m2﹣12=0,
,消去y得:(3+4k2)x2+8kmx+4m2﹣12=0,
设B(x1,y1),C(x2,y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
又A(﹣2,0),由题知kABkAC=![]() =﹣
=﹣![]() ,
,
则(x1+2)(x2+2)+4y1y2=0,且x1,x2≠﹣2,
则x1x2+2(x1+x2)+4+4(kx1+m)(kx2+m)
=(1+4k2)x1x2+(2+4km)(x1+x2)+4m2+4
=![]() +(2+4km)
+(2+4km)![]() +4m2+4=0
+4m2+4=0
则m2﹣km﹣2k2=0,
∴(m﹣2k)(m+k)=0,
∴m=2k或m=﹣k.
当m=2k时,直线BC的方程为y=kx+2k=k(x+2).
此时直线BC过定点(﹣2,0),显然不适合题意.
当m=﹣k时,直线BC的方程为y=kx﹣k=k(x﹣1),此时直线BC过定点(1,0).
当直线BC的斜率不存在时,若直线BC过定点(1,0),B、C点的坐标分别为(1, ![]() ),(1,﹣
),(1,﹣![]() ),满足kABkAC=﹣
),满足kABkAC=﹣![]() .
.
综上,直线BC过定点(1,0).
故答案为:(1,0).


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知p:x∈A={x|x2﹣2x﹣3≤0,x∈R},q:x∈B={x|x2﹣2mx+m2﹣9≤0,x∈R,m∈R}.
(1)若A∩B=[1,3],求实数m的值;
(2)若p是q的充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩卡片游戏:他们手里都拿着分别标有数字1,2,3,4,5,6的6张卡片,各自从自己的卡片中随机抽出1张,规定两人谁抽出的卡片上的数字大,谁就获胜,数字相同则为平局.
(1)求甲获胜的概率.
(2)现已知他们都抽出了标有数字6的卡片,为了分出胜负,他们决定从手里剩下的卡片中再各自随机抽出1张,若他们这次抽出的卡片上数字之和为偶数,则甲获胜,否则乙获胜.请问:这个规则公平吗,为什么 ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() (
(![]() ),且
),且![]() .
.
(1)证明![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,且
,且![]() 证明
证明![]() ;
;
(3)在(2)小问的条件下,若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣blnx在点(1,f(1))处的切线为y=1.
(Ⅰ)求实数a,b的值;
(Ⅱ)是否存在实数m,当x∈(0,1]时,函数g(x)=f(x)﹣x2+m(x﹣1)的最小值为0,若存在,求出m的取值范围;若不存在,说明理由;
(Ⅲ)若0<x1<x2 , 求证: ![]() <2x2 .
<2x2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2+ex﹣ ![]() (x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
A.(﹣ ![]() )
)
B.( ![]() )
)
C.( ![]() )
)
D.( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
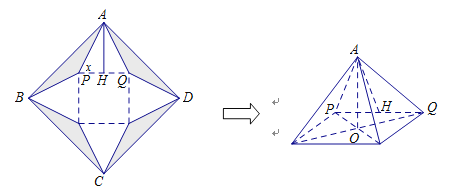
【题目】如图:设一正方形纸片ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥(粘接损耗不计),图中![]() ,O为正四棱锥底面中心.
,O为正四棱锥底面中心.
(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com