
分析 (1)求导,通过对参数b的讨论,确定导函数的正负,判断函数的单调区间.
(2)利用导函数得出函数的极值点,结合函数单调性,通过极值得出a的范围.
解答 解:(1)f′(x)=$\frac{a+b-blnx}{{x}^{2}}$ x>0
令f′(x)=0的x=${e}^{\frac{a+b}{b}}$
令h(x)=a+b-blnx
当b>0时,h(x)递减
x∈(0,${e}^{\frac{a+b}{b}}$),h(x)>0,f′(x)>0,f(x)递增
x∈(${e}^{\frac{a+b}{b}}$,+∞),h(x)<0,f′(x)<0,f(x)递减
当b<0时,h(x)递增
x∈(0,${e}^{\frac{a+b}{b}}$),h(x)<0,f′(x)<0,f(x)递减
x∈(${e}^{\frac{a+b}{b}}$,+∞),h(x)>0,f′(x)>0,f(x)递增
(2)f(x)=$\frac{lnx-a}{x}$
由(1)知,x∈(0,ea+1),f(x)递增
x∈(ea+1,+∞),f(x)递减
f(ea+1)=$\frac{1}{{e}^{a+1}}$位函数的极大值
函数f(x)的图象与函数g(x)=1的图象在区间(0,e]上有公共点
当a+1≤1即a≤0时
$\frac{1}{{e}^{a+1}}$≥1
∴a≤-1
当a+1>1即a>0时
f(e)=$\frac{lne-a}{e}$≥1
∴a≤1-e不成立
故a的范围为a≤-1
点评 考察了利用导函数判断函数的单调性,利用导函数求函数的极值,通过极值判断图象的特征.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
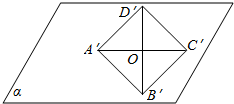 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{2\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3] | B. | (-1,3) | C. | [-1,0)∪(0,3] | D. | (-1,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com