
【题目】设m,n是两条不同的直线,α,β是两个不同的平面,则下列叙述正确的是( )
A.若α∥β,m∥α,n∥β,则m∥n
B.若α⊥β,m⊥α,n∥β,则m⊥n
C.若m∥α,n∥α,m∥β,n∥β,m⊥n,则α∥β
D.若m⊥α,nβ,m⊥n,则α⊥β
【答案】C
【解析】解:在长方体ABCD﹣A′B′C′D′中,
(1)令平面ABCD为平面α,平面A′B′C′D′为平面β,A′B′为直线m,BC为直线n,
显然α∥β,m∥α,n∥β,但m与n不平行,故A错误.
(2)令平面ABCD为平面α,平面ABB′A′为平面β,直线BB′为直线m,直线CC′为直线n,
显然α⊥β,m⊥α,n∥β,m∥n.故B错误.
(3)令平面ABCD为平面α,平面A′B′C′D′为平面β,直线BB′为直线m,直线B′C′为直线n,
显然m⊥α,nβ,m⊥n,但α∥β,故D错误.
故选C.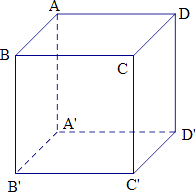
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+ ![]() )(ω>0)的图象的相邻两条对称轴间的距离是
)(ω>0)的图象的相邻两条对称轴间的距离是 ![]() .若将函数f(x)的图象向右平移
.若将函数f(x)的图象向右平移 ![]() 个单位,再把图象上每个点的横坐标缩小为原来的一半,得到g(x),则g(x)的解析式为( )
个单位,再把图象上每个点的横坐标缩小为原来的一半,得到g(x),则g(x)的解析式为( )
A.g(x)=sin(4x+ ![]() )
)
B.g(x)=sin(8x﹣ ![]() )??
)??
C.g(x)=sin(x+ ![]() )
)
D.g(x)=sin4x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河南省部分重点中学2017届高三上学期第一次联考】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 和圆
和圆![]() .
.
(Ⅰ)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)设![]() 为平面直角坐标系上的点,满足:存在过点
为平面直角坐标系上的点,满足:存在过点![]() 的无穷多对相互垂直的直线
的无穷多对相互垂直的直线![]() 和
和![]() ,它们分别与
,它们分别与
圆![]() 和
和![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点![]()
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(2)若![]() 为自然数,则当
为自然数,则当![]() 取哪些值时,方程
取哪些值时,方程![]() 在
在![]() 上有三个不相等的实数根,并求出相应的实数
上有三个不相等的实数根,并求出相应的实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若函数
,若函数![]() 满足:对于给定的
满足:对于给定的![]()
![]() ,存在
,存在![]() ,使得
,使得![]() 成立,那么称
成立,那么称![]() 具有性质
具有性质![]() .
.
(1)函数![]()
![]() 是否具有性质
是否具有性质![]() ?说明理由;
?说明理由;
(2)已知函数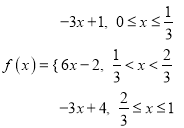 具有性质
具有性质![]() ,求
,求![]() 的最大值;
的最大值;
(3)已知函数![]() 的定义域为
的定义域为![]() ,满足
,满足![]() ,且
,且![]() 的图像是一条连续不断的曲线,问:是否存在正整数n,使得函数
的图像是一条连续不断的曲线,问:是否存在正整数n,使得函数![]() 具有性质
具有性质![]() ,若存在,求出这样的n的取值集合;若不存在,请说明理由.
,若存在,求出这样的n的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知含有![]() 个元素的正整数集
个元素的正整数集![]() (
(![]() ,
, ![]() )具有性质
)具有性质![]() :对任意不大于
:对任意不大于![]() (其中
(其中![]() )的正整数
)的正整数![]() ,存在数集
,存在数集![]() 的一个子集,使得该子集所有元素的和等于
的一个子集,使得该子集所有元素的和等于![]() .
.
(Ⅰ)写出![]() ,
, ![]() 的值;
的值;
(Ⅱ)证明:“![]() ,
, ![]() ,…,
,…, ![]() 成等差数列”的充要条件是“
成等差数列”的充要条件是“![]() ”;
”;
(Ⅲ)若![]() ,求当
,求当![]() 取最小值时
取最小值时![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com