
 某空间几何体的三视图如图所示,则该几何体的体积为$\frac{8-π}{3}$.
某空间几何体的三视图如图所示,则该几何体的体积为$\frac{8-π}{3}$. 分析 由三视图知该组合体是:一个四棱锥沿着右侧面挖去一个半圆锥得到的,由三视图求出几何元素的长度,由锥体的体积公式求出几何体的体积.
解答 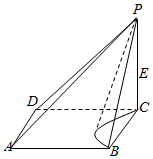 解:由三视图知该几何体的直观图为:
解:由三视图知该几何体的直观图为:
即从四棱锥P-ABCD中挖去了一个半圆锥所得的组合体,
∵四棱锥P-ABCD底面是边长为2的正方形、高为2,
圆锥底面圆的半径是1、高为2,顶点是P,
∴所求的体积V=$\frac{1}{3}×2×2×2-\frac{1}{2}×\frac{1}{3}×π×{1}^{2}×2$
=$\frac{8-π}{3}$,
故答案为:$\frac{8-π}{3}$.
点评 本题考查三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
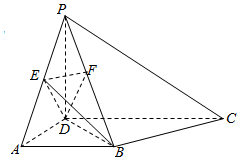 如图,在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,PD=AD=AB=1,CD=2,点E是PA的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,PD=AD=AB=1,CD=2,点E是PA的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是菱形,且∠ABC=60°,侧面PAD是边长为2的正三角形且与底面ABCD垂直.
如图,四棱锥P-ABCD的底面ABCD是菱形,且∠ABC=60°,侧面PAD是边长为2的正三角形且与底面ABCD垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 男生 | 15 | 35 | 50 |
| 女生 | 30 | 40 | 70 |
| 总计 | 45 | 75 | 120 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 微信控 | 非微信控 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.
某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com