【题目】已知锐角△ABC中，角A，B，C的对边分别为a，b，c，b+c=10，a=
，5bsinAcosC+5csinAcosB=3a．
（1）求A的余弦值；
（2）求b和c．
【答案】（1）
；（2）b=c=5
【解析】
（1）把条件5bsinAcosC+5csinAcosB=3a中的边化为角，可求A的正弦值，结合平方关系可得A的余弦值;
（2）利用余弦定理可求.
（1）∵5bsinAcosC+5csinAcosB=3a，
∴由正弦定理可得：5sinBsinAcosC+5sinCsinAcosB=3sinA，
∵sinA≠0，∴5sinBcosC+5sinCcosB=3，可得：sin（B+C）=
，
∵B+C=π
A，∴sinA=，∵A∈（0，
），∴cosA=
=
；
（2）∵a2=b2+c22bccosA=（b+c）22bc（1+cosA），又∵b+c=10，a=
，
∴解得：bc=25，∴解得：b=c=5．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】学校从参加高二年级期末考试的学生中抽出一些学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），所得数据整理后，列出了如下频率分布表．
分组 | 频数 | 频率 |
[40，50） | A | 0.04 |
[50，60） | 4 | 0.08 |
[60，70） | 20 | 0.40 |
[70，80） | 15 | 0.30 |
[80，90） | 7 | B |
[90，100] | 2 | 0.04 |
合计 | C | 1 |
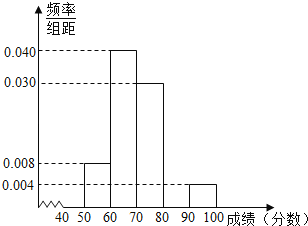
（1）在给出的样本频率分布表中，求A，B，C的值；
（2）补全频率分布直方图，并利用它估计全体高二年级学生期末数学成绩的众数、中位数；
（3）现从分数在[80，90），[90，100]的9名同学中随机抽取两名同学，求被抽取的两名学生分数均不低于90分的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
，（其中
是自然对数的底数）.
(1)若
，求函数
在
上的最大值.
(2)若，关于x的方程
有且仅有一个根，求实数k的取值范围.
(3)若对任意的
、
，
，不等式
都成立，求实数a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在菱形
中，
，
为线段
的中点（如图1）．将
沿
折起到
的位置，使得平面
平面
，
为线段
的中点（如图2）．
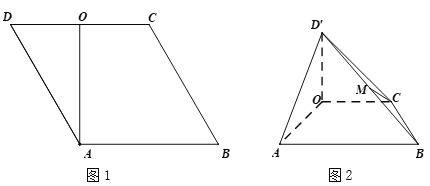
（Ⅰ）求证：
；
（Ⅱ）求证：
平面
；
（Ⅲ）当四棱锥
的体积为
时，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】矩形ABCD中，
，沿对角线AC将三角形ADC折起，得到四面体
，四面体 外接球表面积为
，当四面体的体积取最大值时，四面体的表面积为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《中国诗词大会》是央视推出的一档以“赏中华诗词，寻文化基因，品生活之美”为宗旨的大型文化类竞赛节目，邀请全国各个年龄段、各个领域的诗词爱好者共同参与诗词知识比拼。“百人团”由一百多位来自全国各地的选手组成，成员上至古稀老人，下至垂髫小儿，人数按照年龄分组统计如下表：
分组（年龄） |
|
|
|
频数（人） |
|
|
|
（1）用分层抽样的方法从“百人团”中抽取
人参加挑战，求从这三个不同年龄组中分别抽取的挑战者的人数；
（2）在（1）中抽出的人中，任选
人参加一对一的对抗比赛，求这人来自同一年龄组的概率。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直角梯形ABCD中，
，
，
，
，E为AB的中点.将
沿CE折起，使点B到达点F的位置，且平面CEF与平面ADCE所成的二面角为
.
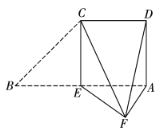
（1）求证：平面
平面AEF；
（2）求直线DF与平面CEF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
