
对于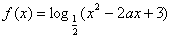 ,
,
(1)函数的“定义域为R”和“值域为R”是否是一回事?分别求出实数a的取值范围;
(2)结合“实数a的取何值时 在
在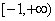 上有意义”与“实数a的取何值时函数的定义域为
上有意义”与“实数a的取何值时函数的定义域为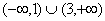 ”说明求“有意义”问题与求“定义域”问题的区别.
”说明求“有意义”问题与求“定义域”问题的区别.
解:记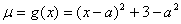 ,则
,则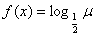 ;
;
(1)不一样;…………………………1分
定义域为R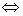
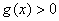 恒成立。
恒成立。
得: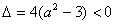 ,解得实数a的取值范围为
,解得实数a的取值范围为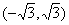 。……………………4分
。……………………4分
值域为R: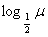 值域为R
值域为R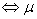 至少取遍所有的正实数,
至少取遍所有的正实数,
则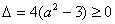 ,解得实数a的取值范围为
,解得实数a的取值范围为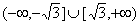 。…………6分
。…………6分
(2)实数a的取何值时 在
在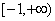 上有意义:
上有意义:
命题等价于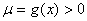 对于任意
对于任意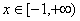 恒成立,
恒成立,
则 或
或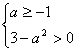 ,解得实数a得取值范围为
,解得实数a得取值范围为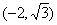 。………………8分
。………………8分
实数a的取何值时函数的定义域为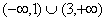 :
:
由已知得二次不等式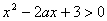 的解集为
的解集为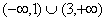 可得
可得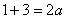 ,则a=2。故a的取值范围为{2}。……………………11分
,则a=2。故a的取值范围为{2}。……………………11分
区别:“有意义问题”正好转化成“恒成立问题”来处理,而“定义域问题”刚好转化成“取遍所有问题”来解决(这里转化成了解集问题,即取遍解集内所有的数值)………12分


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| t |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | an |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.f(x)≥f-1(x) B.f(x)≤f-1(x)
C.f(x)<f-1(x) D.f(x)=f-1(x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com