
如图,在三棱柱ABC-A1B1C1中,已知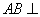 侧面
侧面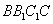 ,AB=BC=1,BB1=2,∠BCC1=
,AB=BC=1,BB1=2,∠BCC1=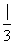 .
.
(1) 求证:C1B⊥平面ABC;
(2)设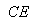 =l
=l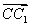 (0≤l≤1),且平面AB1E与BB1E所成的锐二面角
(0≤l≤1),且平面AB1E与BB1E所成的锐二面角
的大小为30°,试求l的值.
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
一个布袋里有3个红球,2个白球共5个球. 现抽取3次,每次任意抽取2个,并待放回后再抽下一次,求:
(1)3次抽取中,每次取出的2个球都是1个白球和1个红球的概率;
(2)3次抽取中,有2次取出的2个球是1个白球和1个红球,还有1次取出的2个球同色的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
体育课的排球发球项目考试的规则是:每位学生最多可发球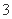 次,一旦发球成功,则停止发球,否则一直发到
次,一旦发球成功,则停止发球,否则一直发到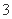 次为止.设某学生一次发球成功的概率为
次为止.设某学生一次发球成功的概率为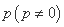 ,发球次数为
,发球次数为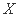 ,若
,若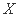 的数学期望
的数学期望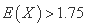 ,则
,则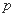 的取值范围是( )
的取值范围是( )

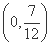

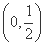

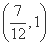


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com